CF852C Property
思维题
题解
OI
题意
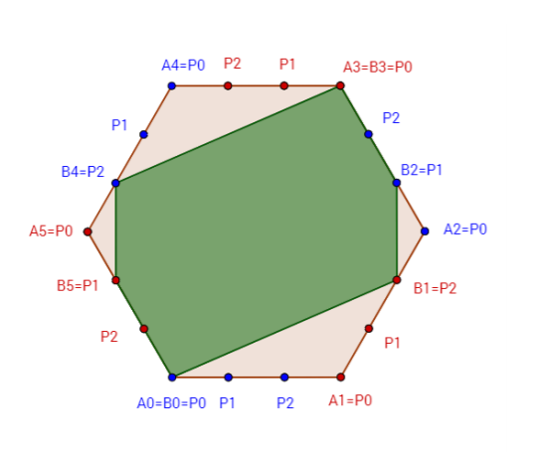
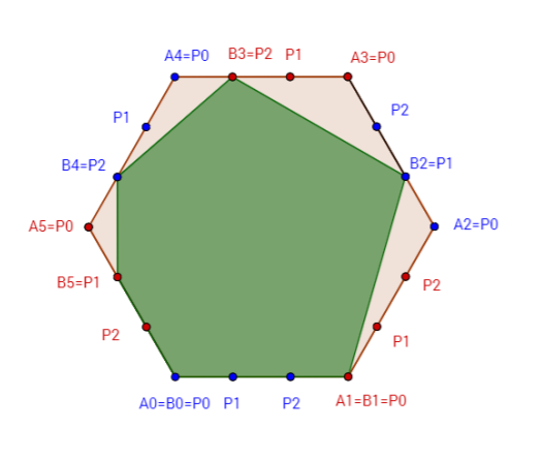
有一个正边形,在每条边上有等分点. 现在已经选定了个点, 个点分别位于第条边上, 且这个点的序号构成了一个排列; 你需要再选出个点位于第条边上, 并且这个点的序号也构成一个排列, 使得这些点构成的多边形面积最大. 输出选择方案.
的一种选法, 蓝色是给定点, 红色是自选点.
以上情况的最优解.
分析
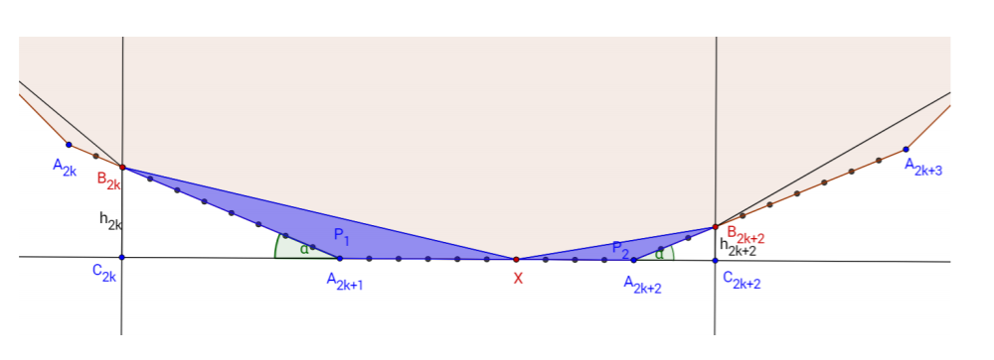
要让保留的面积最大, 就要让删去的面积最小. 考虑计算每一个选择点对删去面积的贡献.
和是给定点, 是动点. 是删去区域的面积.
目的是要最小化, 由于是到的一个排列, 所以应该用小的搭配大的, 就能使总和尽量小.
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| #include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <fstream>
#include <cassert>
#include <cmath>
using namespace std;
typedef long long int64;
const int INF = 0x3f3f3f3f;
const int MAXN = 50000 + 10;
int a[MAXN], b[MAXN], ans[MAXN];
int main() {
int n;
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
b[i] = i;
}
a[n + 1] = a[1];
sort(b + 1, b + n + 1, [](const int& A, const int& B) -> bool {
return a[A] + a[A + 1] < a[B] + a[B + 1];
});
for (int i = 1; i <= n; i++) {
ans[b[i]] = i - 1;
}
for (int i = 1; i <= n; i++) {
cout << ans[i] << ' ';
}
cout << endl;
return 0;
}
|