数值分析作业 - 浮点运算和误差

Problem 1

分析单精度计算 fl(9.4)−fl(9)−fl(0.4) 的结果，并进行计算机实践。

	Symbol	Exponent	mantissa
9.4f	+ 0	3 + 127 = 10000010	100101100110011001100110
9.0f	+ 0	3 + 127 = 10000010	100100000000000000000000
9.4f-9.0f	+ 0	3 + 127 = 10000010	000001100110011001100110
Lsh 5	+ 0	-2 + 127 = 01111101	110011001100110011000000
0.4f	+ 0	-2 + 127 = 01111101	110011001100110011001101
9.4f-9.0f-0.4f	- 1	-2 + 127 = 01111101	000000000000000000001101
Lsh 20	- 1	-22 + 127 = 01101001	110100000000000000000000

得到计算结果为

编写辅助函数用于输出浮点数的比特

#define print_fpbits(x) print_fpbits_impl(x, #x)
template <typename T>
void print_fpbits_impl(T value, std::string expr) {
    auto y = reinterpret_cast<std::uint8_t*>(&value);
    std::cout << expr << ": " << std::endl;
    for (int i = sizeof(T) - 1; i >= 0; i--) {
        char byte = y[i];
        for (int j = 7; j >= 0; j--) {
            std::cout << ((byte >> j) & 1);
        }
    }
    std::cout << std::endl;
}

验证计算过程

print_fpbits(9.4f);
print_fpbits(9.0f);
print_fpbits(0.4f);
print_fpbits(9.4f - 9.0f);
print_fpbits(9.4f - 9.0f - 0.4f);
std::cout << std::format("{:.12f}\n", 9.4f - 9.0f - 0.4f);

得到输出

9.4f: 
01000001000101100110011001100110
9.0f:
01000001000100000000000000000000
0.4f:
00111110110011001100110011001101
9.4f - 9.0f:
00111110110011001100110011000000
9.4f - 9.0f - 0.4f:
10110100110100000000000000000000
-0.000000387430

Problem 2

设计高效的多项式算法 , 计算机编程比较直接算法与优化算法的计算时间（采用双精度进行计算，分别循环 次）

容易写出直接的 多项式计算方法

const double coef[] = {1, 0, 0, 2, 0, 0, 0, 3, 0, 0, 0, 4, 0, 0, 0, 5};

double pow_naive(double x, int n) {
    double res = 1.0;
    for (int i = 1; i <= n; i++) {
        res *= x;
    }
    return res;
}

double f_naive(double x) {
    double res = 0.;
    for (int i = 0; i <= 15; i++) {
        res += coef[i] * pow_naive(x, i);
    }
    return res;
}

和简单的 优化

double f_fast(double x) {
    double res = 0.;
    double pow = 1.;
    for (int i = 0; i <= 15; i++) {
        res += coef[i] * pow;
        pow *= x;
    }
    return res;
}

需要注意的是, 针对 C++ 一类编译器具有强大静态优化能力的编程语言, 将简单的算法在同样的输入下单纯地重复运行并不是合理的性能测量方式, 因为编译器很容易将整个循环删除掉. 简单起见, 可以在循环中要求从 std::vector 中读取并存储数据, 以防止无用的循环被删除. 下面报告程序在 MSVC 19.33.31629.0 下, 简单循环 次的用时

x = 2, naive: 2272.14ms
x = 2, fast: 418.473ms
x = 2.22... naive: 2245.62ms
x = 2.22..., fast: 426.92ms

启用 /O2 优化后, 性能有显著的提升

x = 2, naive: 686.996ms
x = 2, fast: 113.86ms
x = 2.22... naive: 670.233ms
x = 2.22..., fast: 108.462ms

Problem 3

推导计算 的递推公式,用正向和逆向递推计算 ，比较并分析两种迭代的误差和稳定性。

容易推导公式

初始值可以取

这个正向递推公式每次递推将误差放大五倍

forward = (NestList[{E - #[[2]] #[[1]], #[[2]] + 1} &, {1., 2}, 20] // Transpose)[[1]];
forward // InputForm

{1., 0.7182818284590451, 0.5634363430819098, 
 0.4645364561314058, 0.395599547802016, 0.34468454164694906, 
 0.30549003693040166, 0.27436153301583177, 0.24902803131655915, 
 0.22800151529345358, 0.21026516023105568, 0.19509990568637692, 
 0.18198305453614516, 0.17051906495301283, 0.1604958541638526, 
 0.15034816183740363, 0.16236307722318344, -0.2042535615582568, 
 6.599099498065924, -129.26370813285942, 2717.256152618507}

注意到在 16 项处由于误差的累积导致积分有界性已被破坏, 之后的迭代过程明显不收敛.

考虑反向迭代公式

取 反向迭代

backward = (NestList[{1/#[[2]] (E - #[[1]]), #[[2]] - 1} &, {1., 30}, 
      29] // Transpose)[[1]] // Reverse;
backward // InputForm

{1., 0.7182818284590452, 0.5634363430819095, 
 0.4645364561314071, 0.3955995478020096, 0.3446845416469873, 
 0.30549003693013366, 0.27436153301797606, 0.24902803129726034, 
 0.2280015154864418, 0.21026515810818536, 0.19509993116082064, 
 0.18198272336837695, 0.17052370130176742, 0.16042630893253398, 
 0.15146088553850115, 0.14344677430452524, 0.13623989097759062, 
 0.12972389988482333, 0.12380383076257832, 0.11840138244490007, 
 0.1134514146712435, 0.10889929102044421, 0.10469884396838404, 
 0.10081072924944416, 0.09720286797349674, 0.09380439317463288, 
 0.09175881956932448, 0.057276060948634834, 1.}

与 NIntegrate 直接积分 (保证 20 位有效数字) 的结果比较并绘制图像

direct = 
 Table[NIntegrate[x^n E^x, {x, 0, 1}, AccuracyGoal -> 20, 
   WorkingPrecision -> 20], {n, 1, 20}];
ListLinePlot[{forward, backward, direct}]

20230312161016

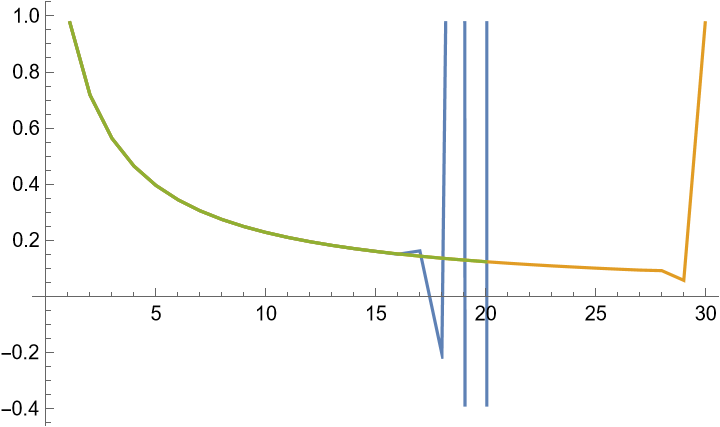
绘制两种算法和直接数值积分法的残差

ListLinePlot[
 Abs[{Take[forward, 20] - direct, Take[backward, 20] - direct}]]

20230312161441

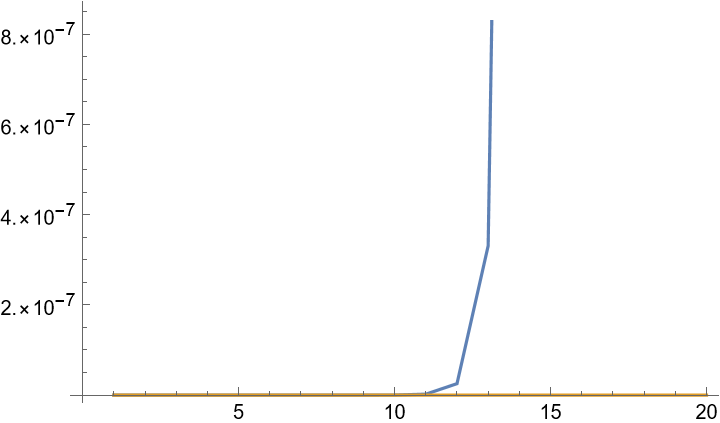
由于反向迭代逐渐减小误差的特性, 表现远好于正向迭代