数值分析作业 - 非线性求解方程
数值分析Problem 1

分析收敛阶:
- 二分法每步将误差缩小
, 线性收敛, 收敛阶为 , - 割线法收敛阶为
- 不动点迭代
, 收敛阶为 , - 不动点迭代
, 收敛阶为 , - 牛顿法收敛阶为
先比较收敛阶大小, 收敛阶为
Problem 2

则牛顿法对应的不动点迭代
Problem 3

Problem 4

则
Problem 5
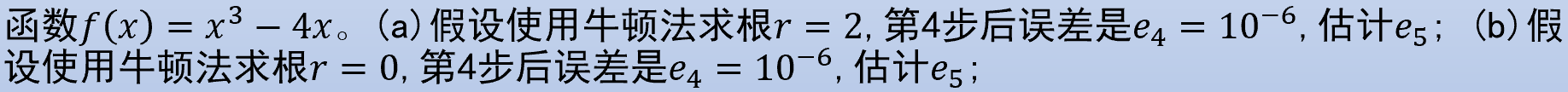
则牛顿法局部二次收敛, 有
估计
估计
Problem 6

Problem 7

二分法
1 | precision = 10; |
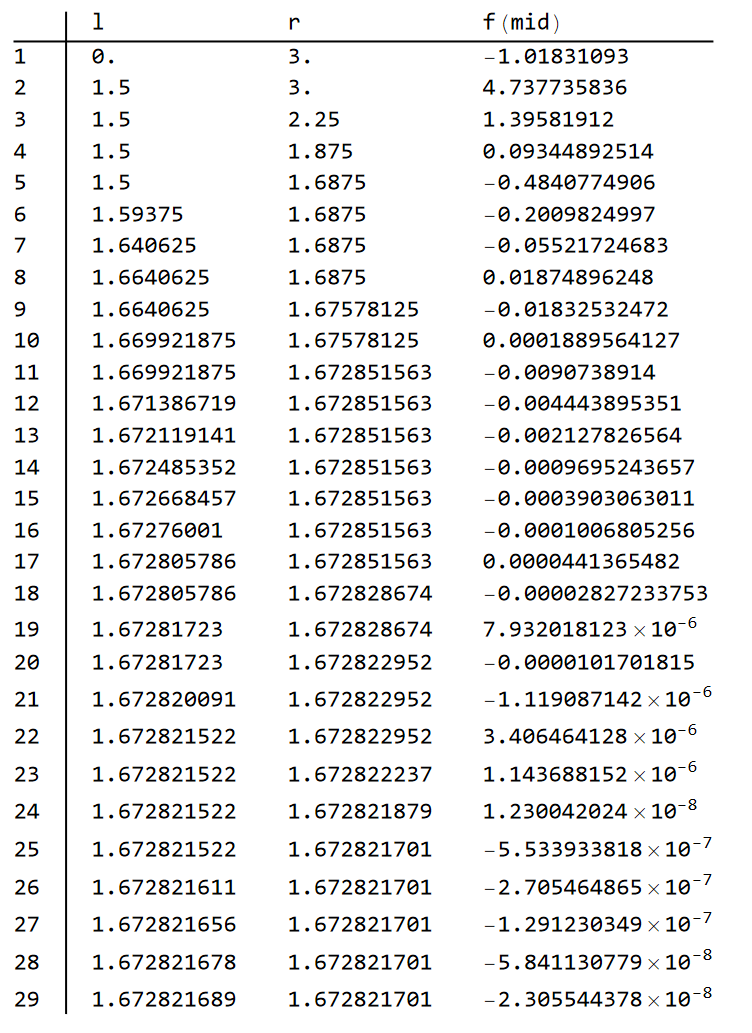
不动点迭代
构造一种可行的不动点迭代形式
1 | NestList[Log[7 - #] &, 0., 20] // InputForm |
1 | {0., 1.9459101490553132, 1.6201977869925166, 1.6826516101163946, |
牛顿法
1 | NestList[# - (E^# + # - 7)/(E^# + 1) &, 0., 20] // InputForm |
1 | {0., 3., 2.2371293658878337, 1.7930473102816238, 1.6787764832017877, |
试位法
1 | tryPosition[fun_, var_, l0_, r0_, it_] := Module[{f, l, r, c, n}, ( |
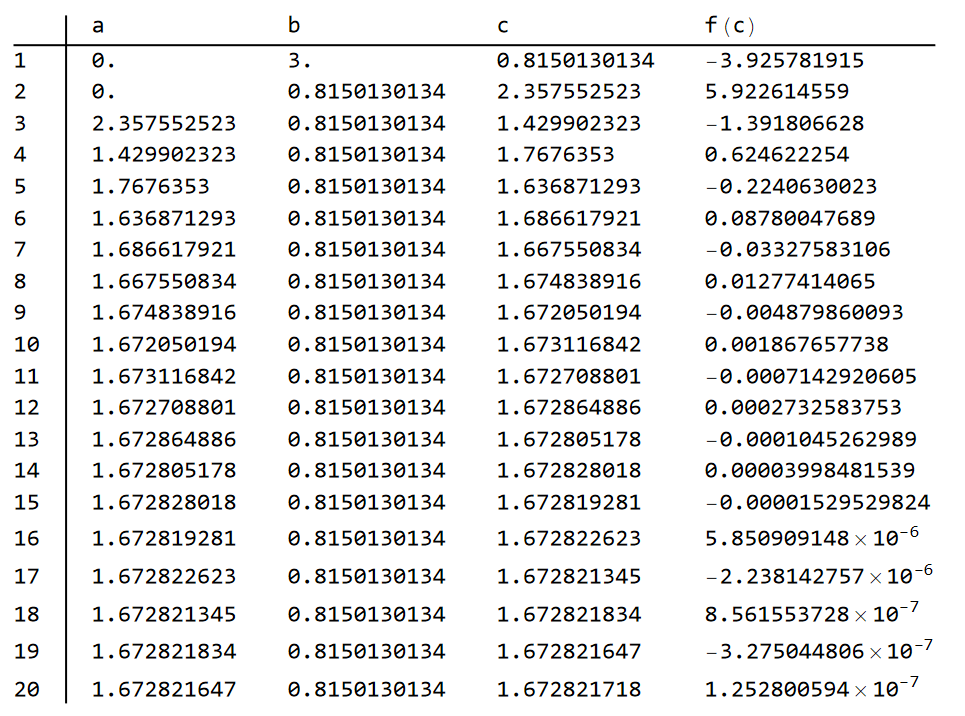
关于收敛性的比较: 运行结果表明所有的方法都能收敛到唯一的零点. 与 NSolveValue 直接求解的结果作比较, 绘制绝对误差的绝对值 (对数尺度纵坐标):
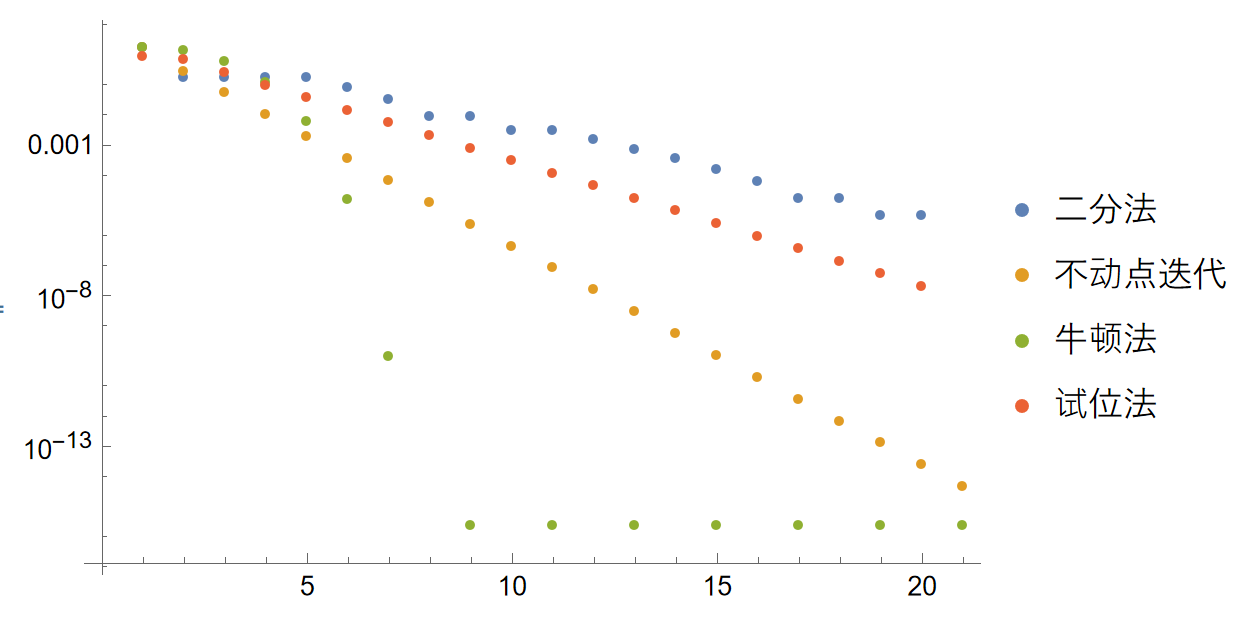
可以看出不同算法的收敛速度, 从快到慢排序:
- 牛顿法
- 不动点迭代
- 试位法
- 二分法
