CSP 初赛数学复习
数学数学逻辑记号
| 与 | 或 | 非 |
|---|---|---|
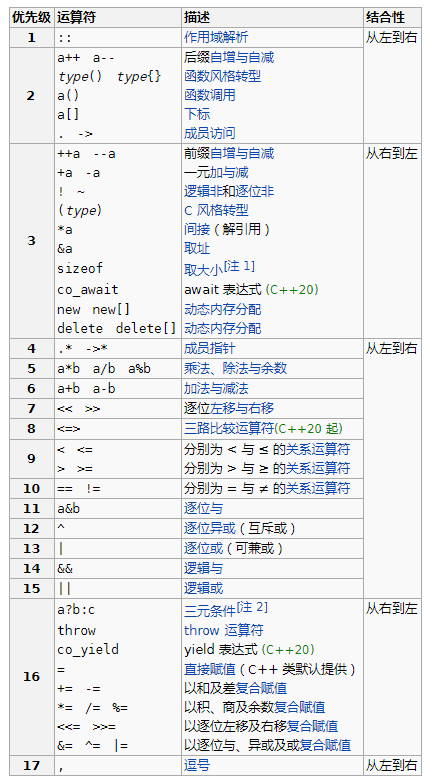
C++ 运算符优先级:
排列组合
排列的定义: 从
组合的定义: 从n个不同元素中, 任取m个元素, 并成一组, 叫做从n个不同元素中取出m个元素的一个组合.
与顺序有关的用排列, 与顺序无关的用组合
加法原理, 乘法原理.
一些重要思想
学校师生合影,共8个学生,4个老师,要求老师在学生中间,且老师互不相邻,共有多少种不同的合影方式?
插入法: 对于要求某几个元素不相邻的问题, 可以考虑先排好其他的元素, 而对于不相邻的元素从其他元素排好后的的序列中枚举空位插入. 答案:
5个男生3个女生排成一排,3个女生要排在一起,有多少种不同的排法?
捆绑法: 要求相邻的元素可以视作一个元素参加排列, 注意捆绑的元素内部也能产生排列. 答案:
袋中有不同年份生产的5分硬币23个, 不同年份生产的1角硬币10个, 如果从袋中取出2元钱, 有多少种取法?
剩余法: 硬币共有2.15元, 取出两元即留下0.15元, 可以是
学校安排考试科目9门, 语文要在数学之前考, 有多少种不同的安排顺序?
对等法: "语文在数学之前"和"语文在数学之后"的情况是等价的, 所以答案就是
某个班级共有43位同学, 从中任抽5人, 正、副班长、团支部书记至少有一人在内的抽法有多少种?
排异法: 用总情况数减去三人都不选的情况, 避免分类讨论. 答案:
将8个相同的球放入3个不同盒子中, 每个盒子至少放一个, 有几种方法?
隔板法: 7个空位放2个板, 有
将8个相同的球放入3个不同盒子中, 盒子可以为空, 有几种方法?
隔板法: 两块板 + 8个球共10个元素, 方法数相当于从10个位置里选两个放板, 所以有
隔板法和插空法的区别: 隔板法要求球相同
特殊的排列组合问题
圆排列: 从n个不同的元素中取r个沿一圆周排列.
有重复元素的排列: 分别有
递推关系
错排问题
第i个元素不在i位置上的排列总数. 考虑两种情况:
- 先错排前
第一类 Stirling 数
n个不同元素构成m个圆排列的方案数. 考虑第n个元素:
- 单独组成一个圆排列
- 插到之前
第二类 Stirling 数
将n个不同的元素拆分成m个集合的方案数.
n个有区别的球放到m个相同的盒子中, 要求无一空盒, 其不同的方案数用
- 令
- 把
注意隔板法是相同球进不同盒, 这里是不同球进相同盒.
Catalan 数
推荐阅读: 卡特兰数 — 计数的映射方法的伟大胜利
令
一个足够大的栈的进栈序列对应的出栈序列的种数: 考虑最后出栈的是第i个元素, 所以比i先出栈有
n个节点的二叉树种类数: 考虑中序遍历的序列, 树根为i, 则左子树的方案数为
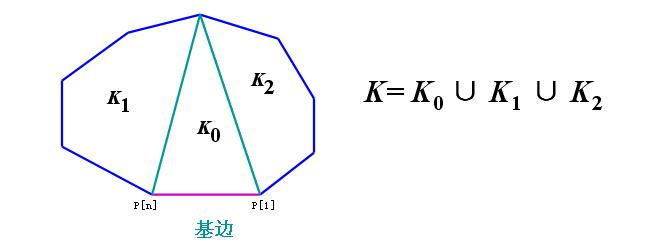
凸多边形的三角形划分: 一个凸的n边形, 用直线连接他的两个顶点使之分成多个三角形, 每条直线不能相交, 问一共有多少种划分方案. 解法见图:

由n对括号形成的合法括号表达式数: 类比出栈序列.
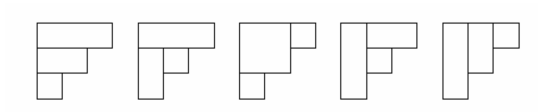
用n个长方形去填充一个高度为n的阶梯图形的方法数:

考虑包含最左上角的方块的矩形对应的是哪一个阶梯, 然后分为下边和右边两部分, 得到卡特兰数的递推公式.
集合取数问题
设
- 要放第n个数, 所以不能放第
- 不放第n个数
也可以用插空法模型来解决问题.
整数划分问题
将整数n分成k份, 且每份不能为空, 不考虑顺序互不相同的方法数. 令
- 分出来的k份每一份都大于一, 所以先从n中取出k来摊在每一份上, 再分了剩下的
- 分了一个1出来. 剩下的再说.
自然数n的拆分方案:
特征根法
数列
为得到其函数形式, 需将两边整理为类似
即
经过化简可得到
其中
不动点法
数列
令
若
则
若
则
时间复杂度
NOIP2017 D1T2
P, NP, NPC, NP-Hard
推荐阅读: P问题、NP问题、NP完全问题和NP难问题
| 简称 | 英文 | 定义 | 例子 |
|---|---|---|---|
| P问题 | P: polynominal | 存在多项式时间算法的问题 | 冒泡排序 |
| NP问题 | NP: Nondeterministic polynominal | 能在多项式时间内验证一个正确解的问题 | TSP |
| NPC问题 | NPC: Nondeterminism Polynomial Complete | 存在这样一个NP问题, 所有的NP问题都可以约化成它. (只要解决了这个问题, 那么所有的NP问题都解决了) | 逻辑电路问题(给定一个逻辑电路, 问是否存在一种输入使输出为False), Hamilton 回路, TSP |
| NP 难问题 | NP Hard | 所有的NP问题都能约化到它, 但是他不一定是一个NP问题 | 并没有 |
我们感兴趣NP问题是否都是P问题(P == NP?)(如果是的, 那么所有NP问题都可以用计算机来解决了), 在研究这一点的过程中, 我们发现了一类特殊的NP问题, 解决它就可以解决所有的NP问题, 称之为NPC问题. 解决NP-Hard问题也可以解决NP问题, 但是NP-Hard问题不一定是NP问题.
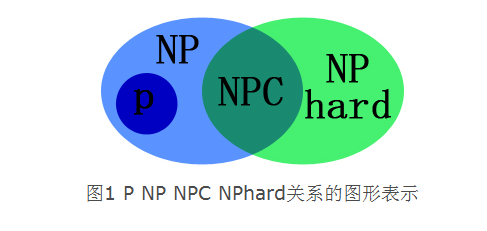
P=NP至今仍未被证明或推翻, NPC问题的发现使得情况更加微妙了.
Master 定理
推荐阅读: Master 定理学习笔记
| 记号 | 意义 |
|---|---|
| 等于 | |
| 小于等于 | |
| 小于 | |
| 大于等于 | |
| 大于 |
记不到就都当做一样的就是了
简单来说, 如果一个算法的时间复杂度能表示为一个如下所示的递推关系式:
那么
如
如
存在一个非负整数
如
简单来说就是