概统速通 - 大数定理

随机变量序列的收敛性

几种收敛性的关系

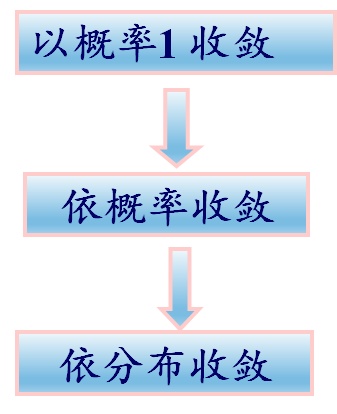
分布函数弱收敛

定义 对于分布函数列 如果存在非降函数 使得

在 的每一个连续点上都成立, 则称 弱收敛于 , 记为

这样得到的极限函数是有界的非降函数, 但不一定是分布函数.

定理 正极限定理: 分布函数列弱收敛于分布函数, 则相应的特征函数列收敛于特征函数, 且在 的任意有限区间一致收敛.

特征函数一致连续, 特征函数收敛即为逐点收敛

定理 逆极限定理: 特征函数列收敛于某一函数 且 在 连续, 则分布函数列弱收敛于分布函数, 且 是 的特征函数

求特征函数的极限时, 遇到指数套指数等情形, 使用 Taylor 展开.

依分布收敛

用分布函数列收敛来定义随机变量序列收敛.

定义 随机变量序列 的分布函数列 弱收敛于 的分布函数 , 称 依分布收敛 于 (随机变量或常数), 记为

或 或

依概率收敛

仿照数列收敛定义随机变量序列收敛

定义 设 是定义在 上的随机变量序列, 若 有

或

称 依概率收敛 到 , 记为

或

很大时, 与 出现较大偏差的可能性很小, 有很大把握保证 和 很接近

几乎处处收敛

仿照函数列收敛定义随机变量序列收敛. 随机变量是样本空间上的实值函数. 但是要求 ,

条件太强, 考虑弱化.

定义 设 是定义在 上的随机变量序列, 若存在随机变量或函数 使得

即

称随机变量序列 以概率 1 收敛于 或几乎处处收敛于 , 记为

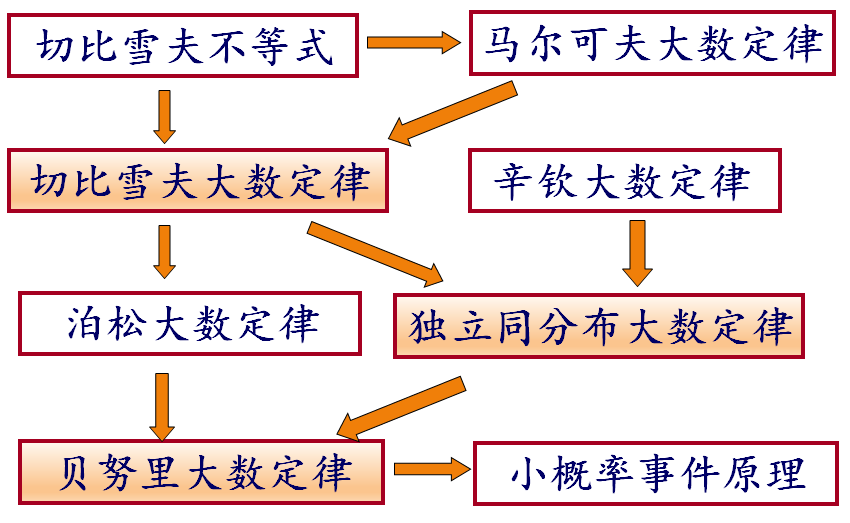
大数定律

弱大数定律的关系

定义 弱大数定律: 设随机变量序列 中每一项的期望 都存在, 若

则称其服从弱大数定律.

前 项的算术平均值将紧密的聚集在其期望附近 对应的随机变量收敛 而不是

贝努利大数定律

定理 设 是 次重复独立试验中事件 发生的频率, 是事件 在每次实验中发生的概率, 则 , 即

此定理以严格的数学形式描述了频率的稳定性: 试验次数 很大时, 事件发生的频率将紧密的聚集在其概率附近

定理 独立同分布变量序列 ,

则

小概率事件原理

概率很小的事件, 在一次试验中几乎是不可能发生的, 从而在实际中可看成不可能事件.

独立同分布大数定律

独立同分布的随机变量序列, 每一项的均值和方差存在 (且相等), 则服从弱大数定律.

切比雪夫大数定律

独立, 期望存在, 方差一致有界的随机变量序列服从弱大数定律.

泊松大数定律

独立随机变量序列

服从弱大数定律

辛钦大数定律

独立同分布变量只要数学期望存在就服从大数定律.

马尔科夫大数定律

随机变量序列只要满足

就服从大数定律.

强大数定律

定义 弱大数定律: 设随机变量序列 中每一项的期望 都存在, 若

则称其服从强大数定律.

服从强大数定律 服从弱大数定律

• 博雷尔强大数定律: 服从强大数定律
• 科尔莫哥洛夫判别法: 独立随机变量序列 服从强大数定律
• 科尔莫哥洛夫定理: 独立同分布随机变量序列满足 服从强大数定律

中心极限定理

定义 随机变量序列独立且存在有限数学期望和方差

随机变量序列服从中心极限定理 前 项和的标准化随机变量序列依分布收敛到标准正态分布.

服从中心极限定理的随机变量序列可进行概率的近似计算

中心极限定理解释了哪些随机变量可认为是服从正态分布的

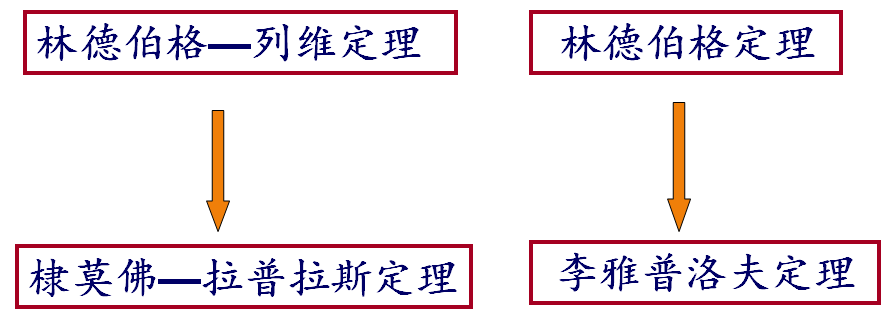
定理 林德伯格—列维定理 (独立同分布中心极限定理): 独立同分布随机变量序列 , 服从中心极限定理

多个独立同分布变量之和近似服从正态分布

定理 棣莫佛—拉普拉斯定理 随机变量序列

服从中心极限定理

随机变量序列 , , 则 很大的二项分布可近似看成正态分布, 一般要求

定理 林德伯格: 独立随机变量序列满足林德伯格条件,

其中 , 则服从中心极限定理, 即

保证各随机叠加项一致的小. 大量一致的小的随机变量的近似正态分布.

定理 李雅普洛夫定理: 随机变量序列满足

服从中心极限定理.

许可协议

本文采用 署名-相同方式共享 4.0 国际 许可协议，转载请注明出处。

分享文章