复变函数速通 - 积分

简单闭曲线的方向: 正向对应内部在左侧 (外边界逆时针, 内边界顺时针). 复定积分的定义类似实数域上的 Riemann 定积分, 只是不在区间上, 而是在光滑的有向曲线上划分分点.

对积分路径的划分

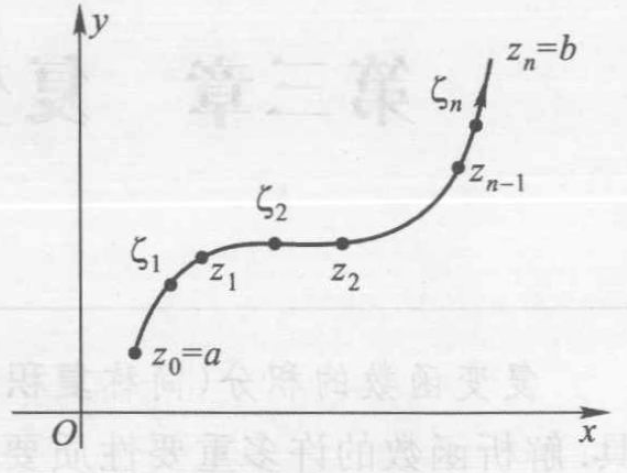
定理 可积的条件: 连续, 光滑 可积

在形式上可以视作 与 相乘

分实部, 虚部转化为两个二元实变函数的线积分

复积分仍具有实积分的线性性, 可加性等性质, 注意积分估值不等式

若 有上界 :

说明

绕奇点的圆周上的积分

Cauchy 积分定理

定理 在单连通域 内处处解析, 则 沿 内任意一条封闭曲线 的积分为零.

若 连续, 则利用 Green 公式和 C-R 方程容易说明. 在不连续时也成立. 另有推论

1. 若 是 的边界, 易得只需在闭区域 上解析就有结论成立
2. 事实上, 只需要在 内解析, 在 上连续就有结论成立

闭路变形原理

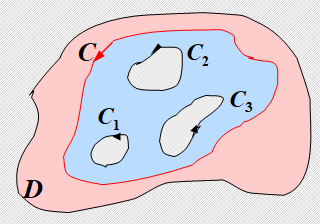
定理 闭路变形原理: 解析函数沿闭曲线的解纷, 不因闭曲线在区域内连续变形 (不经过不解析点) 而改变.

复合闭路定理

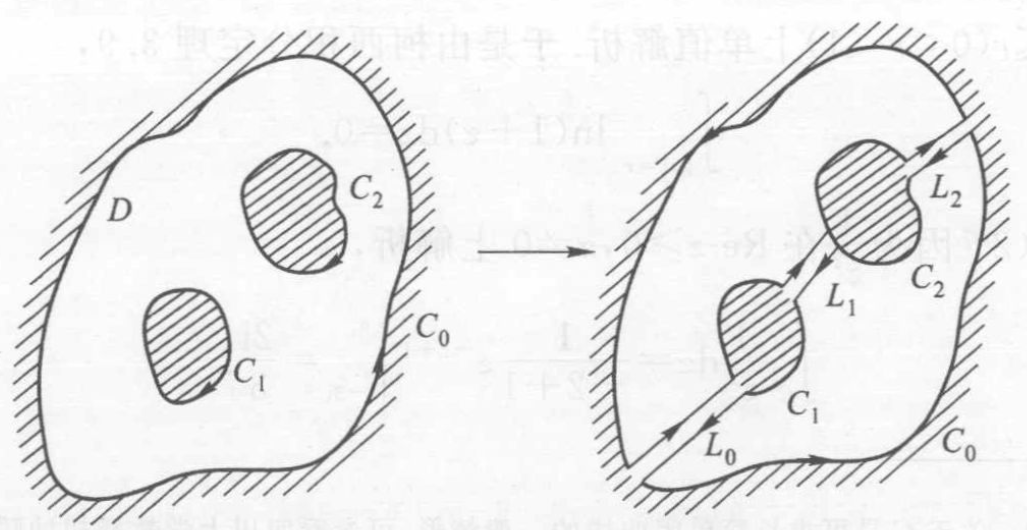
定理 复合闭路定理: 在 内解析, 各自绕一个奇点

1. 沿外边界积分等于沿内边界积分之和
2. 是由 正向, 反向组成的复合曲线

可将 的结论推广到绕奇点的任意简单闭曲线上.

不定积分

定理 在单连通域 内处处解析, 积分 与路径无关

定理 变上限求导: 在单连通域 内处处解析, 是 内解析函数,

定义 原函数: 在 内导数为 , 称 是 的原函数. 的任意两个原函数相差一个常数.

有类似实数的 Newton-Lebiniz 公式.

Cauchy 积分公式

定理 在区域 内处处解析, 为 内任意一条正向简单闭曲线且内部完全包含于 内, 为 内任意点, 则

解析函数在区域内的值可用边界上的积分来表示. 公式也提供了计算解析函数积分的方法.

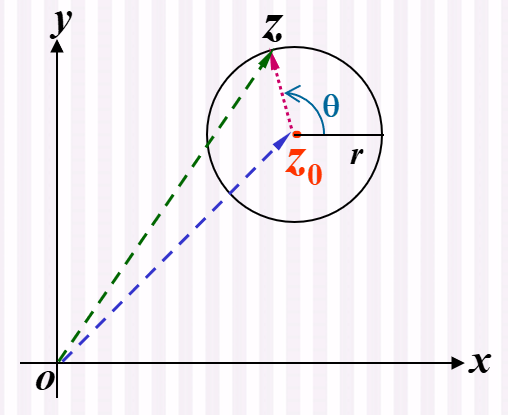
定理 解析函数的平均值定理: 解析函数在圆心处的值等于在圆周上的平均值.

定理 解析函数的无穷可微性: 解析函数的导数仍然是解析函数. 解析函数的 阶导数:

通过高阶导数公式, 利用求导来计算积分

定理 Morera 定理: 在单连通区域 内连续, 且对于区域内任意周线 在区域内解析

Cauchy 不等式

定理 在 内解析, 圆周 及其内部包含于 , 则

其中

定义 整函数: 在整个复平面上都解析的函数

定理 Liouville 定理: 有界整函数必为常数

利用 Liouville 定理可证明代数学基本定理: 平面上,

必有零点.

调和函数

定义 调和函数: 二元实变函数在区域内具有二阶偏导数, 满足 Laplace 方程

定义 共轭调和函数: 是调和函数,

定理 解析函数 的虚部 是实部 的共轭调和函数

偏积分法:

不定积分法:

许可协议

本文采用 署名-相同方式共享 4.0 国际 许可协议，转载请注明出处。

分享文章