数值分析速通 - 线性问题
线性方程组的直接解法
高斯消元
得到左侧上三角阵, 回代求解. 消元复杂度
LU 分解
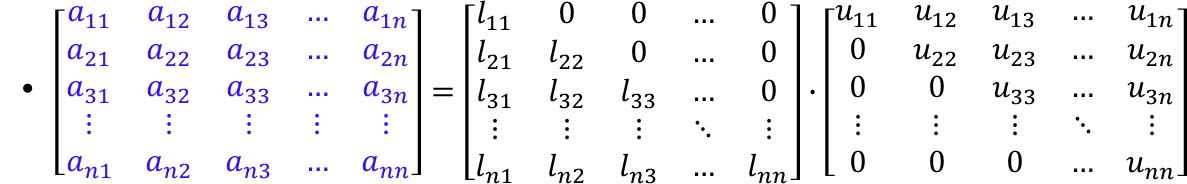
LU 分解不唯一, 可规定对角线上元素为 1
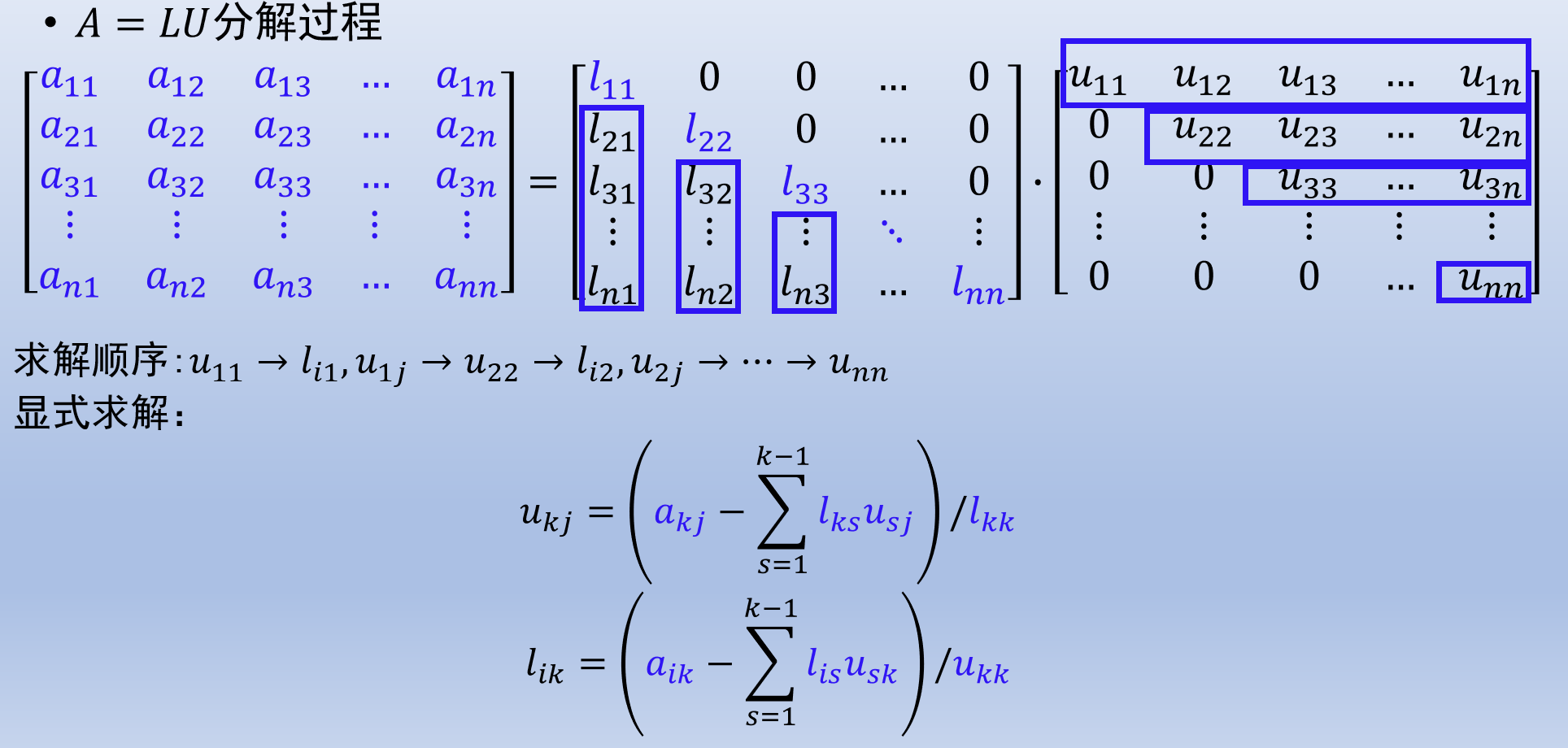
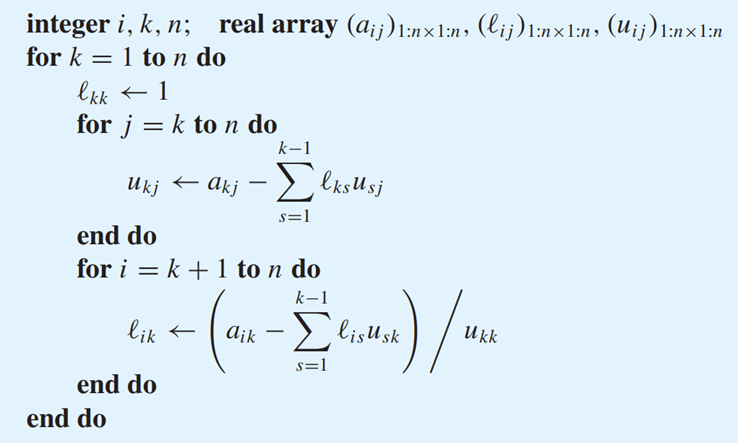
LU 分解定理:
误差
算子范数
最大绝对列和 , 的谱半径 (特征值最大模) 的平方根 最大绝对行和
求解
- 近似解
的前向误差 - 后向误差
- 误差放大因子
- 条件数: 求解
时对于所有 可能出现的最大误差放大因子
定理: 可逆方阵的条件数为
前向和后向误差满足
联系
顺序高斯消元
顺序高斯消元后, 左侧的上三角阵为
列主高斯消元增加
严格行对角占优矩阵: 对角线元素比这一行其他元素加起来大
定理：不选主元Gauss消元法保持矩阵的严格行对角占优性质
推论：行对角占优矩阵非奇异且有 LU 分解
线性方程组的迭代法
迭代矩阵
不同的迭代方法的区别为构造了不同的
Richardson 迭代
Jacobi 迭代
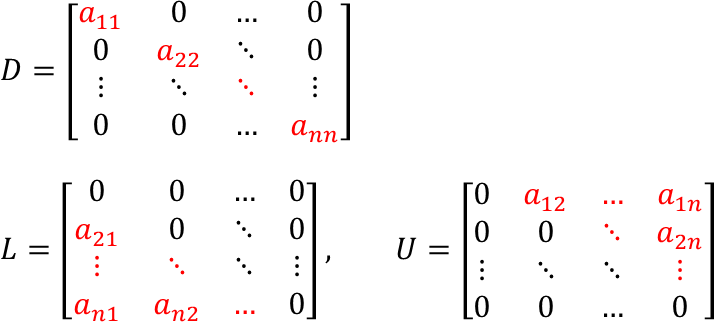
Gauss-Seidel 迭代
主对角元非零收敛
SOR 迭代
添加 "动量" 项
即
Gauss-Seidel 迭代推广到 SOR 迭代形式
欠松弛 Gauss-Seidel 超松弛
需要实验确定收敛最快的
主对角元非零,
对称正定线性方程组的解法
若
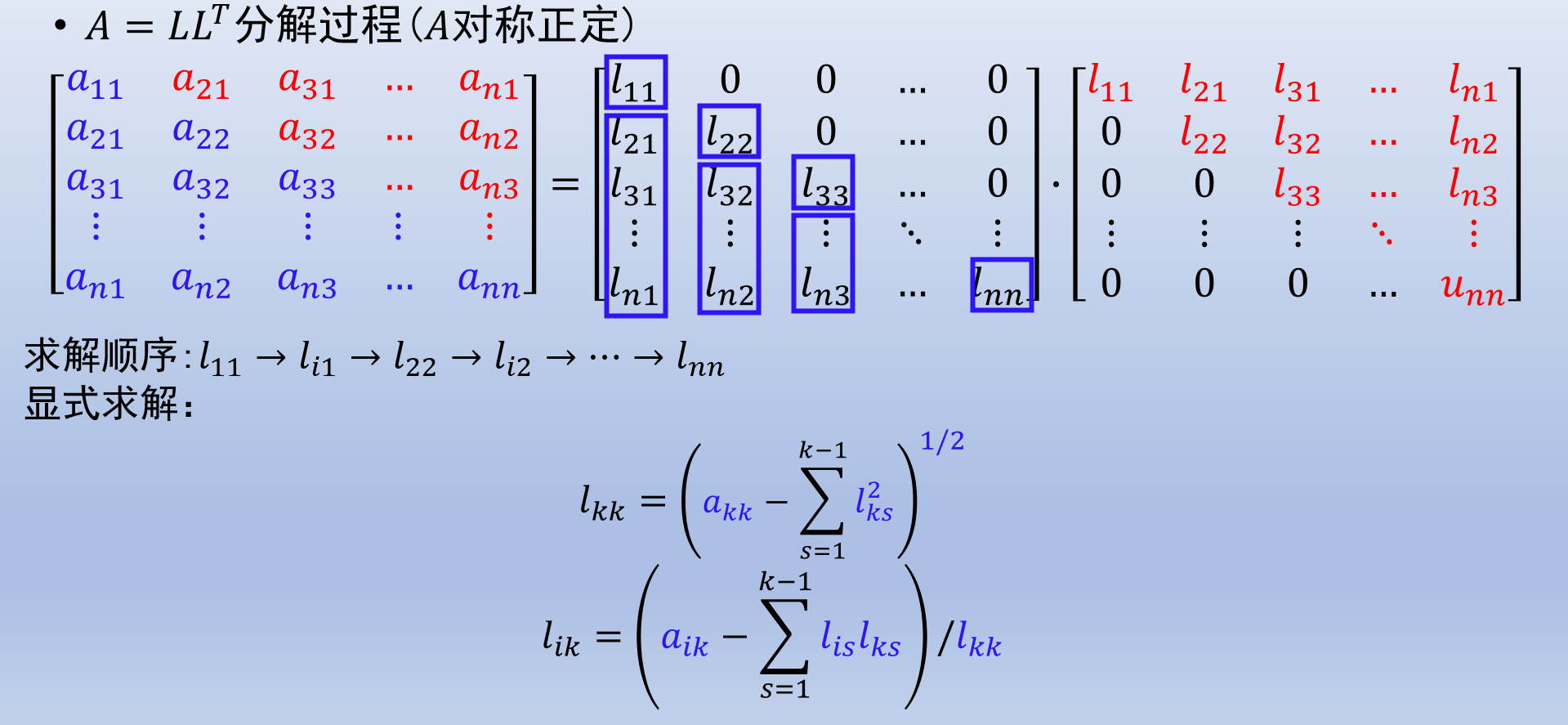
Cholesky 分解
实对称正定矩阵可以分解为
梯度下降法
其中
梯度下降法迭代公式.
共轭梯度法
矩阵特征值的数值解法
通过高次多项式求根解特征值是病态问题, 需要更好的方法
盖尔圆盘
通过盖尔圆盘可估计特征值的大概范围
盖尔(Gershgorin)圆盘定理：方阵
说明
对
圆心是对角线元素, 半径是每一行的和.
则特征值位于
盖尔(Gershgorin)圆盘第二定理：设方阵
- 推论1：严格对角占优矩阵可逆。
- 推论2：方阵的
个盖尔圆盘两两互不相交，则相似于对角阵。 - 推论3：实方阵的
个盖尔圆盘两两互不相交，则特征值全为实数。
扰动矩阵特征值圆盘定理：若
通过条件数估计特征值偏离的范围.
幂法
将矩阵反复作用于一个向量, 最终方向会接近于矩阵的一个特征向量. 将向量
当
特征向量
特征值
线性收敛率
若最大特征值是两重,
特征值
特征向量
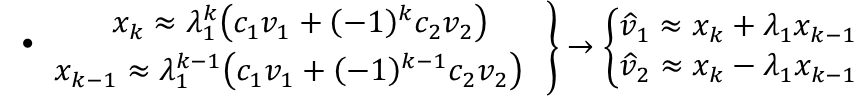
通过以上方法求出模长最大的特征向量. 求解其他特征向量
- 模长最小:
- 离
最远: - 离
最近:
Rayleigh 商迭代
已知近似特征向量
最小化残差 Rayleigh 商
QR 分解
把
- 消减 QR 分解:
( 的列向量不够多, 没有求出完整的正交基) - 完全 QR 分解:
(任意补充 个向量得到完整正交基, 矩阵多余的部分补零)
Gram-Schmit 正交化
对
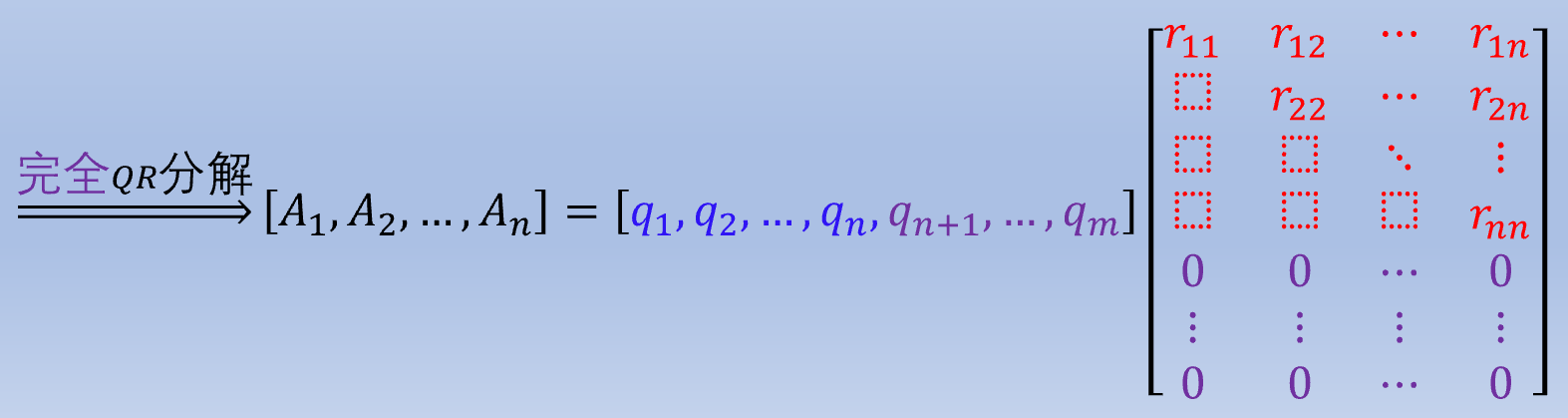
两种形式在数学上等价, 但如果因为数值计算的误差导致靠前的向量之间没有完全正交, 改进的方法仍然能尽量保持后面的向量之间的正交性.
时间复杂度:
Householder 变换
则
利用 Householder 变换实现 QR 分解, 方法是通过叠加多个 Householder 反射子得到
由
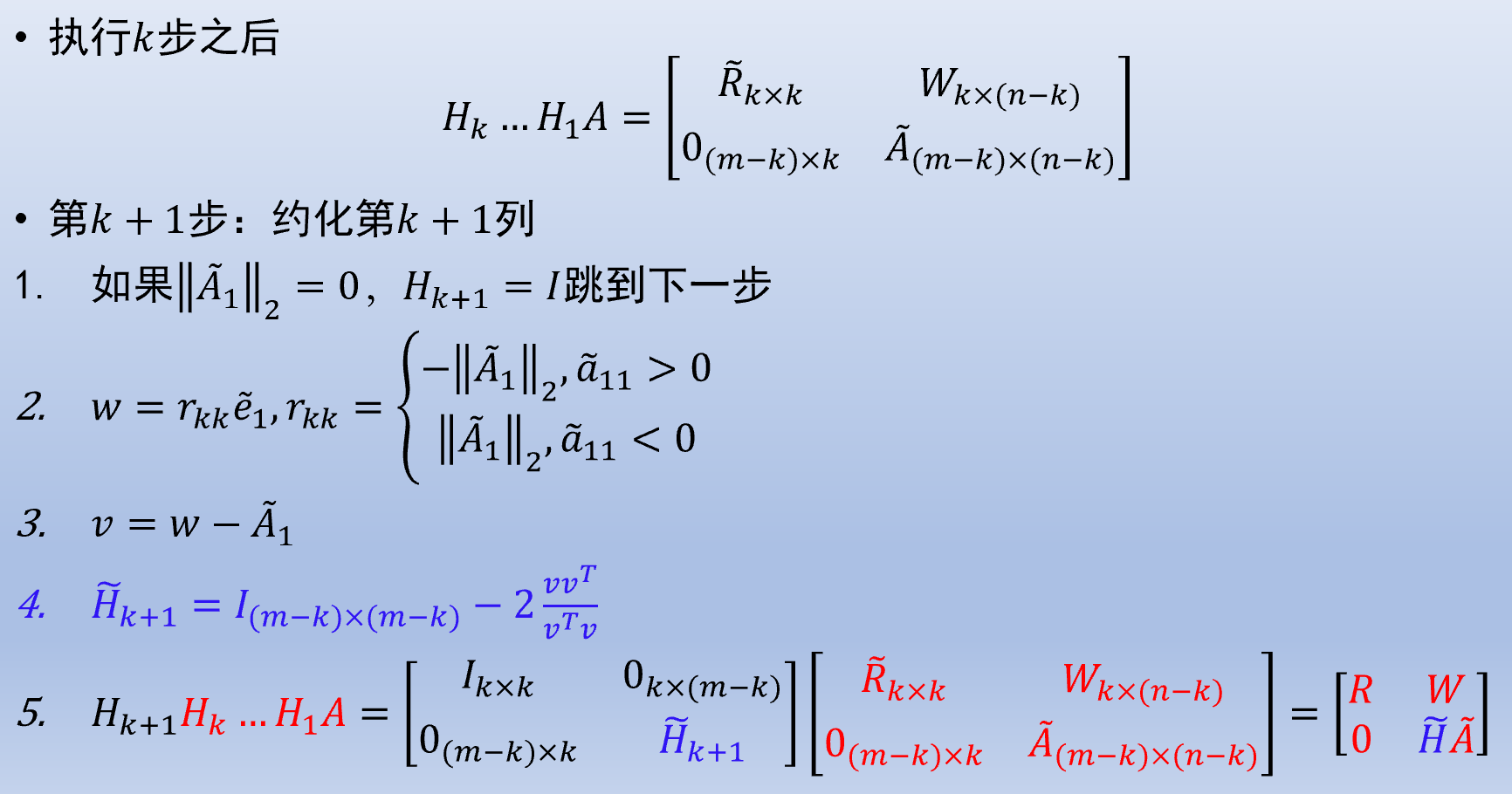
Householder 变换直接得到的是完全 QR 分解, 数值稳定性比 GS 正交化好.
QR 算法
求出矩阵的所有特征值. 选取一组正交向量同时进行幂迭代，每次迭代都对向量进行正交化，最终可得到所有的特征向量及对应的特征值.
本文采用 署名-相同方式共享 4.0 国际 许可协议，转载请注明出处。
