数值分析速通 - 非线性问题
插值
插值问题的数学定义:
求

基本多项式插值
很显然, 选取相同的插值结点, 多项式插值的
多项式插值
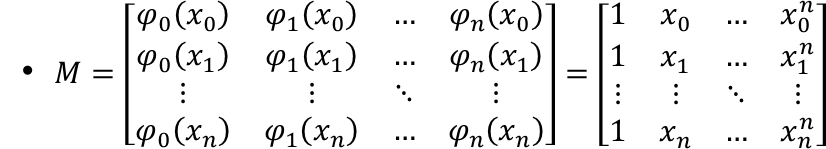
形式简单, 但是系数矩阵条件数大
Lagrange 插值
构造一组多项式基函数
容易得到
满足条件,
Lagrange 插值不用求解
Newton 插值
希望能够增量计算新的插值节点, 而不改变之前插值结点的系数, 方便计算. 选取基函数
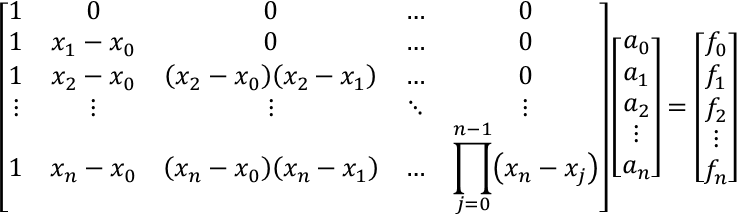
规定记号
为


得到系数
Chebyshev 插值
Motivation
多项式插值误差定理:
其中
这个形式显然是 Taylor 展开的 Lagrange 余项
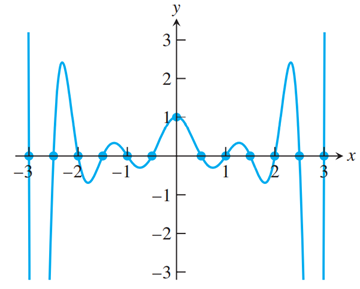
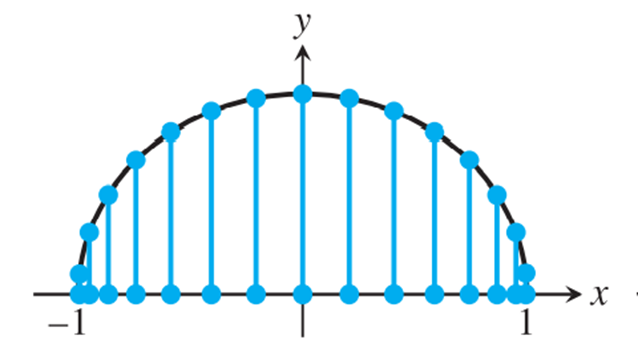
进行高次多项式插值的弊端, 高阶导数
性质
第一类

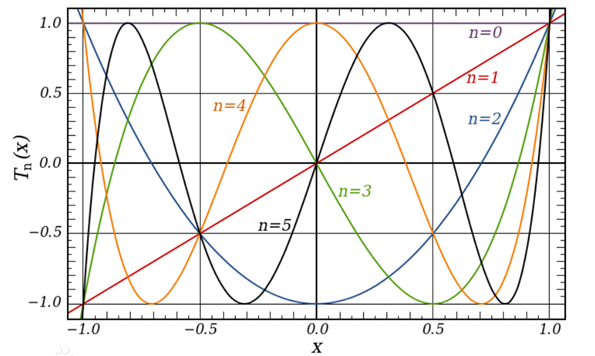
证明

说明
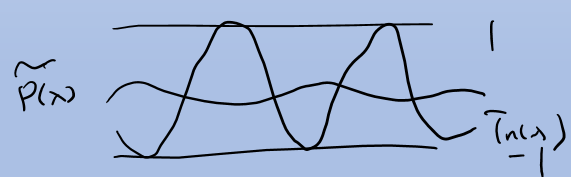
反证: 设首一多项式
是
在标准区间
把标准区间变换到任意区间
误差满足
Hermite 插值
除了插值结点处的函数值, 把一阶导数值等也纳入插值方程. 需要根据选取的方程条件数量确定插值的次数, 防止无解或多解.
Hermite 插值定理:存在唯一的次数至多是
只有一个插值结点, 条件是 0 至

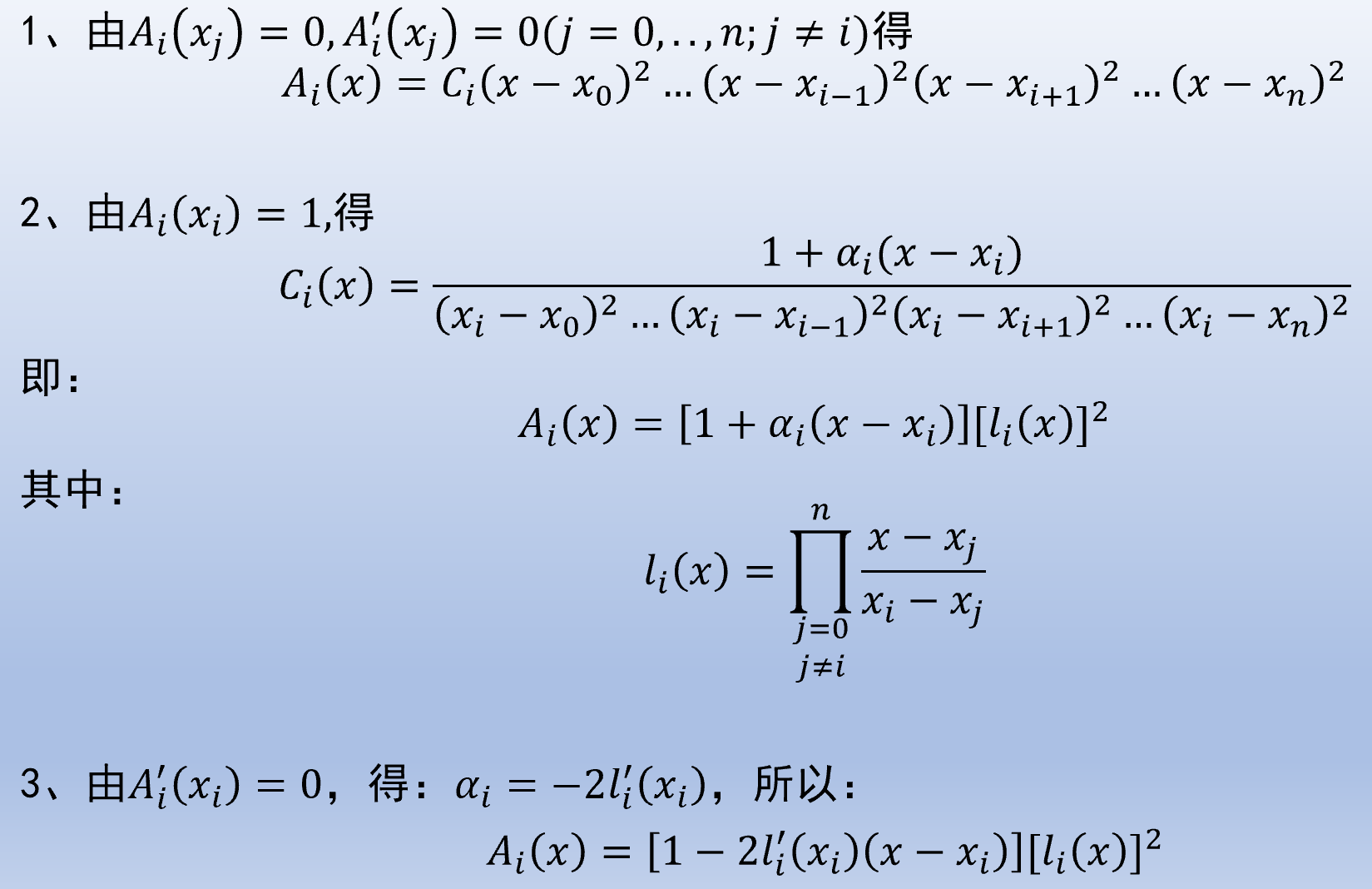
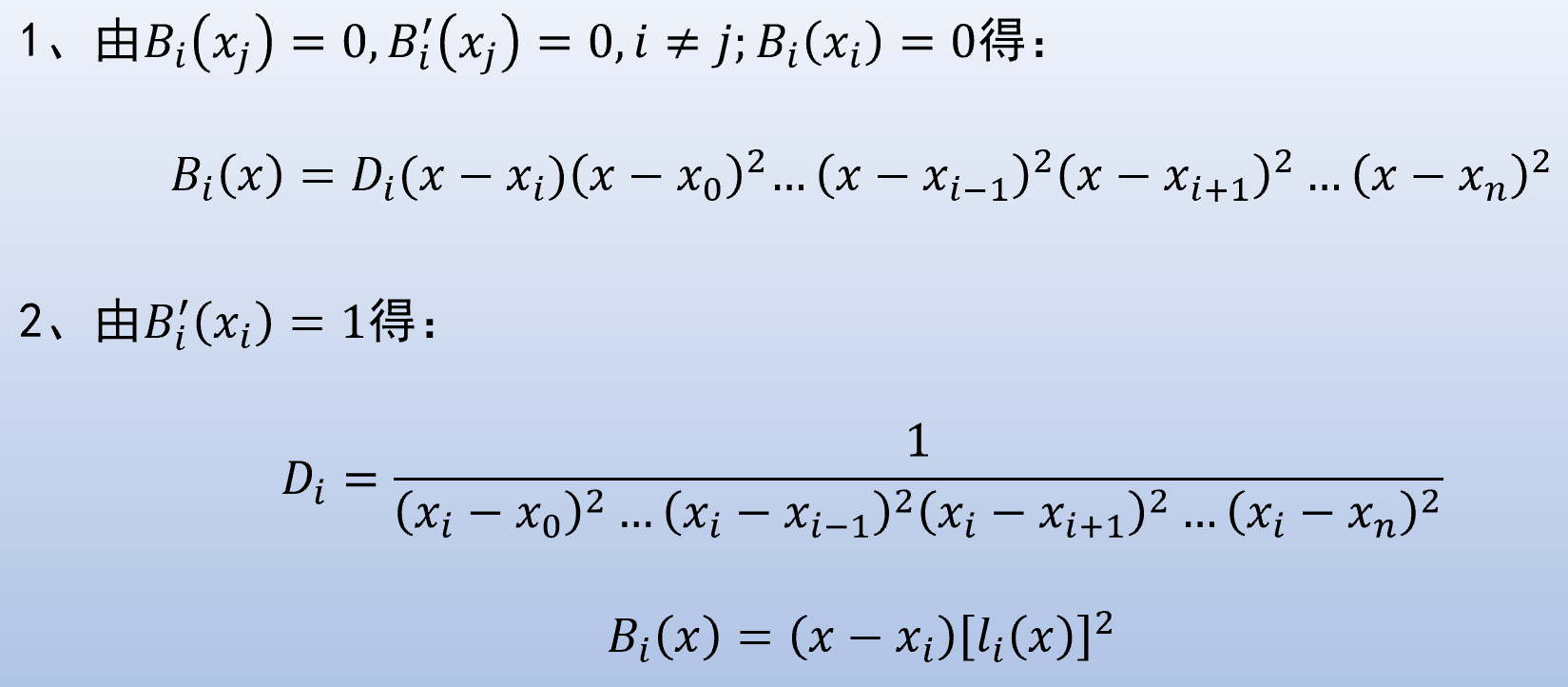
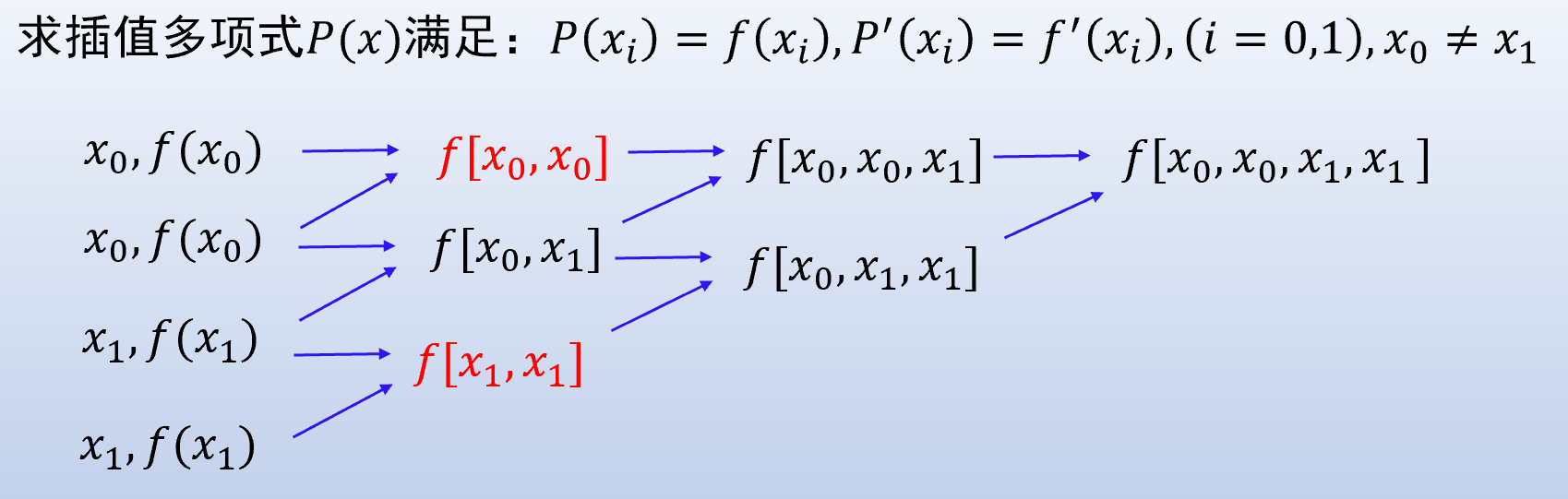
直接把已知的

样条插值
高次多项式插值有种种问题, 还是分段用低次多项式近似吧.
节点
- 在每个子区间
- 在整个区间
零次样条插值即为分段常数函数, 一次样条为分段线性函数, 常用三次样条
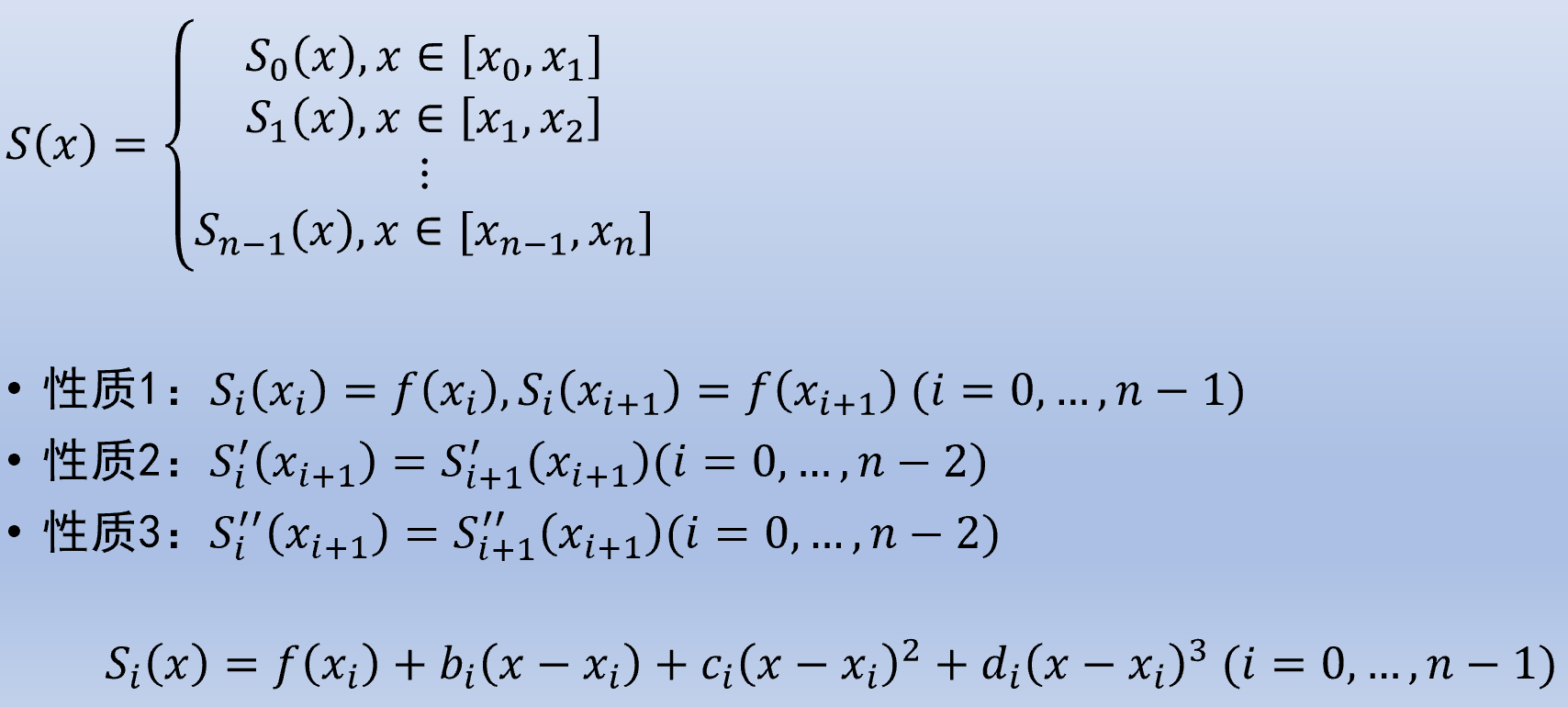


数据拟合与最小二乘
数据拟合也是用基函数线性组合, 但不要求精确过每个点, 要求曲线到给定数据点的距离最小


求解最后的矩阵就能得到最小二乘拟合系数. 最后的矩阵可以写作

法线方程
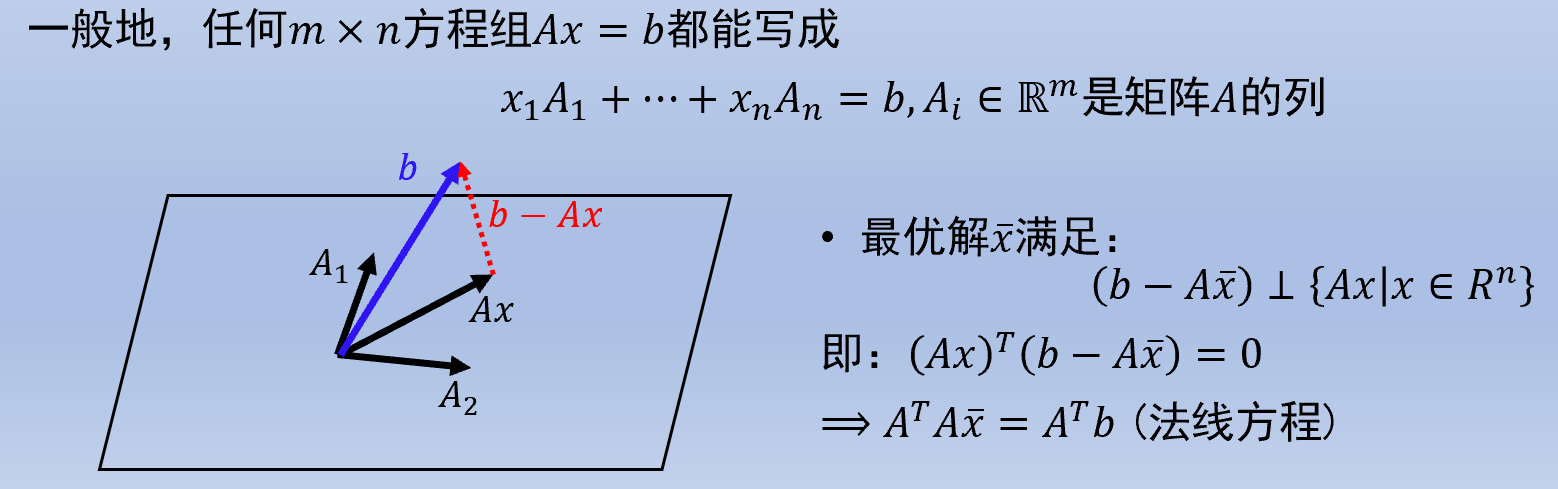
公式被称作法线方程, 是超定方程
对于非线性问题的最小二乘拟合, 需要选取合适的基函数, 还可能需要取对数来线性化.
QR 分解
直接使用法线方程计算最小二乘解数值不稳定. 可利用 QR 分解来求解.
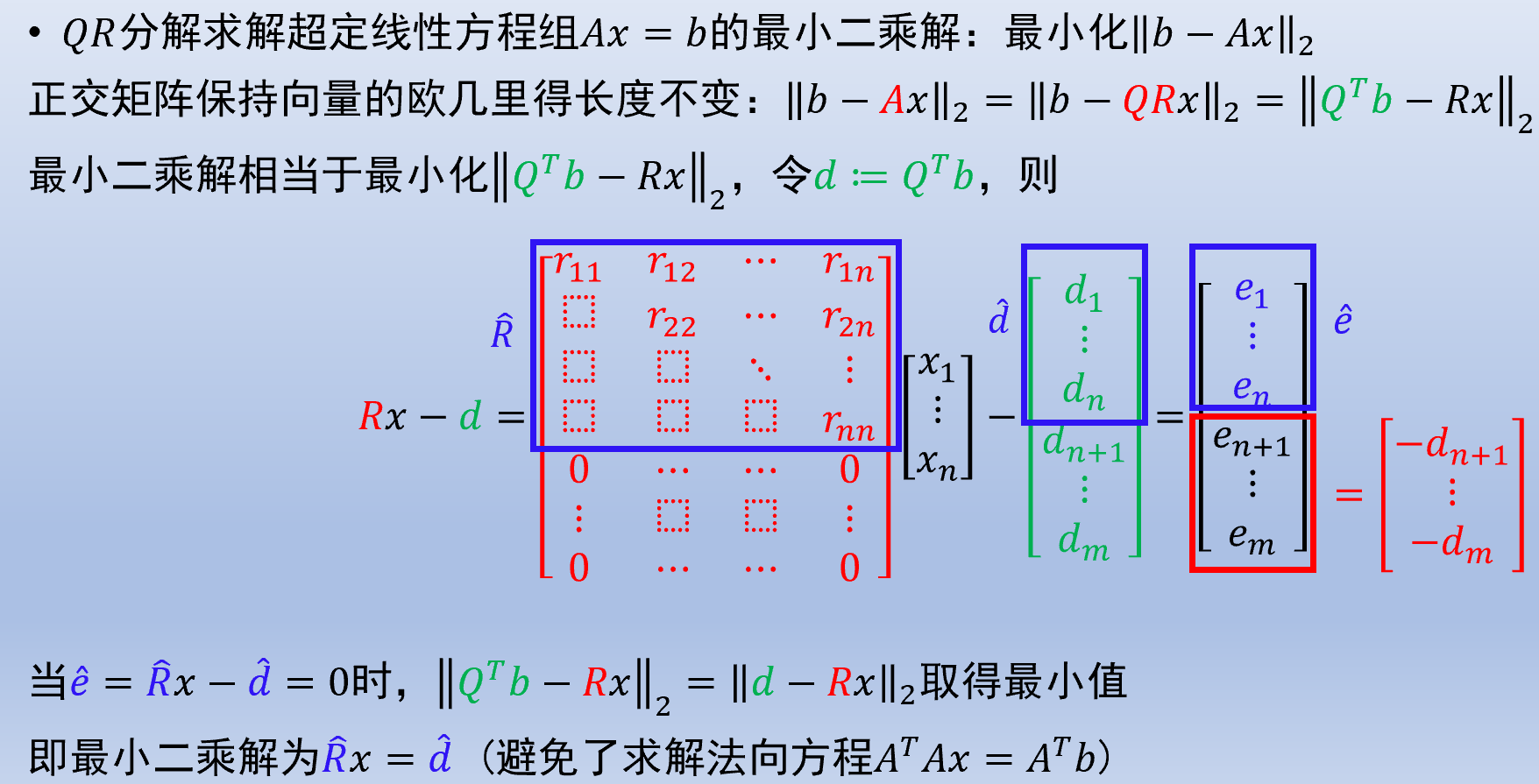
只需进行完全 QR 分解, 然后求解
数值微分
直接似是而非的去个小量
- 前向差商
- 后向差商
- 中心差商
- 二阶中心差商
用多项式插值的导数近似函数的导数. 两点插值得到的就是前向 / 后向差商, 三点插值得到中心差商
误差分析
通过 Taylor 展开的 Lagrange 余项控制误差的范围. 正确的差商公式都是 Taylor 展开式的变形 (确定插值点, 可以通过 Taylor 展开得到唯一正确的差商公式, 以及余项).

由于数值计算误差的存在,
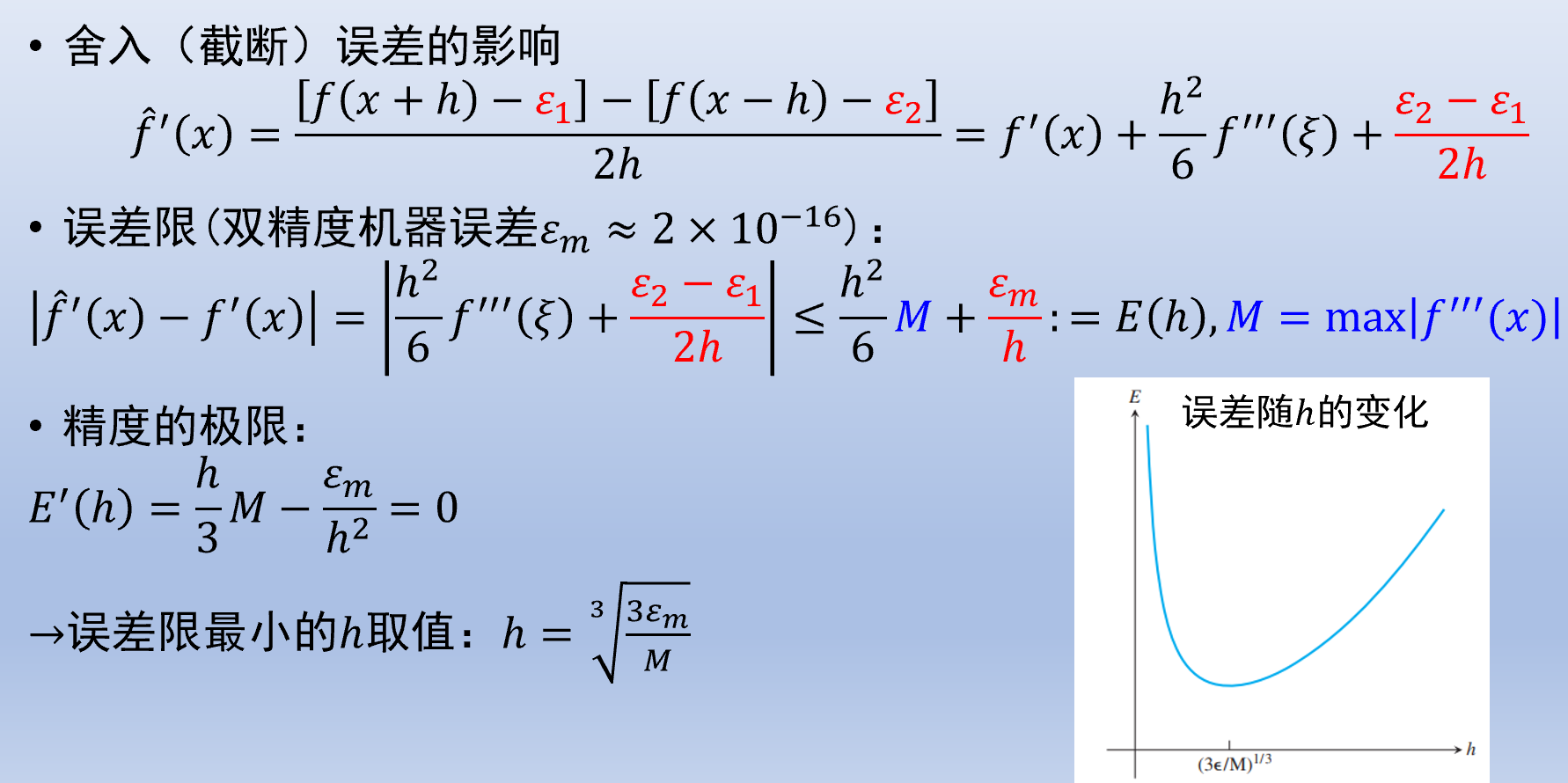
Richardson 外推
对任何
都能再加一项缩减一半步长
至少是
待定系数法

给定插值点, 可以通过 Taylor 展开得到唯一正确的差商公式, 以及余项. 插值点数量已知时, 为了让这个方程有唯一解, Taylor 公式展开的阶数是确定的, 余项的阶数也能确定了. 解线性方程组求出系数后再带回展开式, 可能余项的系数为 0, 这时差商公式会具有更高的阶数.
数值积分
Newton-Cotes 积分
用插值函数的积分来近似原函数的积分, 积分节点等距的插值型数值积分称为 Newton-Cotes 积分. 在区间
数值积分的代数精度, 指可以准确积分的多项式的最高阶数. 给定积分的插值结点, 可以根据插值结点数量确定至少具有的代数精度, 并列线性方程组解出唯一正确的积分系数.
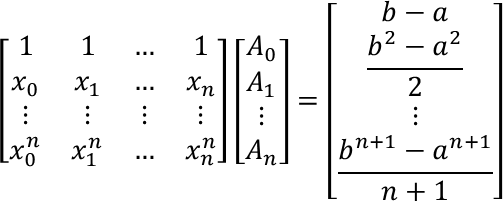
从插值误差
插值误差
一般形式的 Newton-Cotes 积分
- 梯形法则: 两点一次插值
- Simpson 法则: 三点二次插值
- 中心法则: 使用中点函数值
- 三点开 Newton-Cotes 积分:
复合 Newton-Cotes 积分, 先把
- 复合中心法则
- 复合梯形法则
- 复合 Simpson 法则
Romberg 积分
用 Richardson 外推法提高复合梯形法则的精度.



Gauss 积分
非均匀地选取插值结点, 使积分值具有尽可能高的数值精度. 可通过正交基构造.


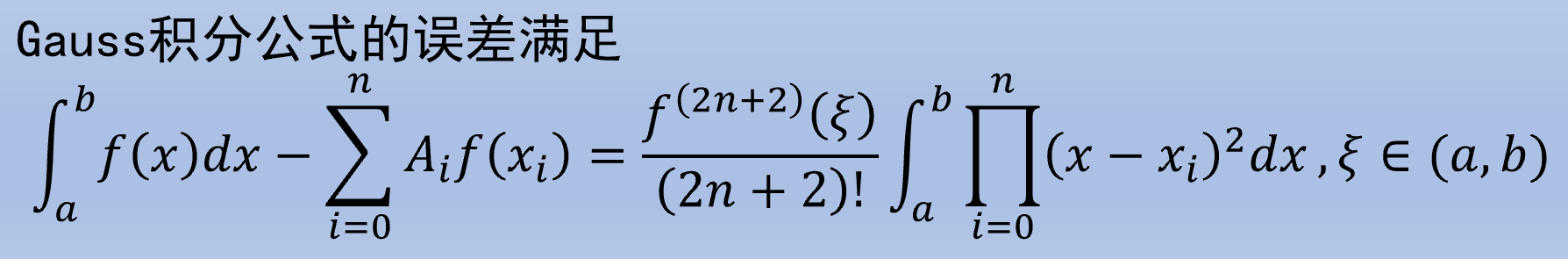
找到
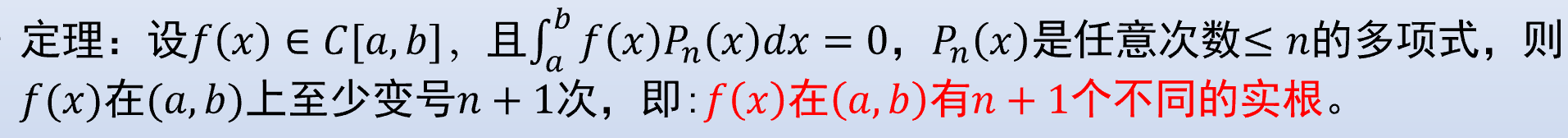
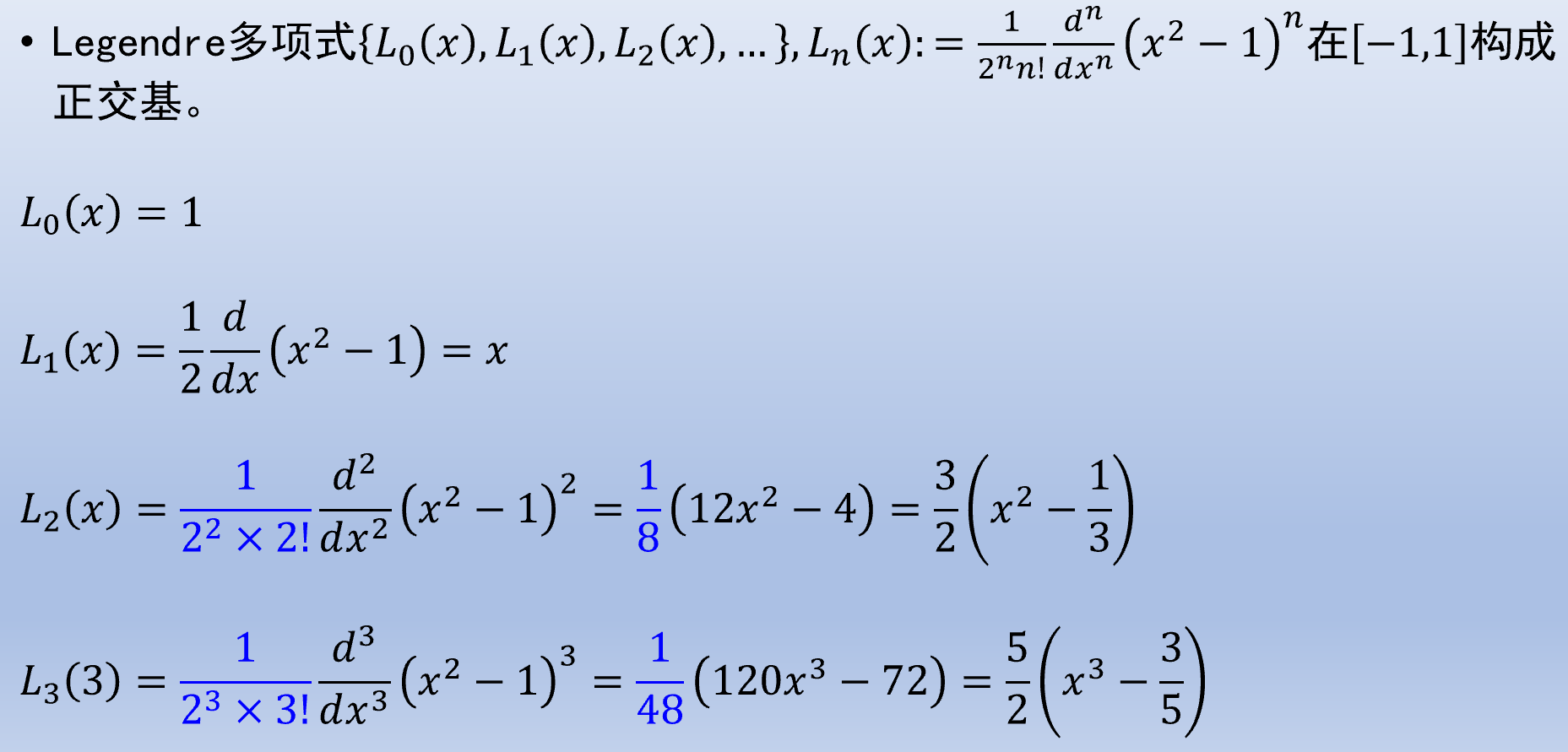
Legendre 多项式是合适的构造.

定义映射
把
