数分速通 - 函数极限

Heine 定理

定理 含于 内, 以 为极限的数列 , 相应的函数值数列收敛到

定理 存在 含于 内, 以 为极限的数列 , 相应的函数值数列极限 存在

只需说明函数值数列极限一定存在, 可证明其相等. 可推广到左右极限及其他极限过程

函数极限 Cauchy 收敛

定理 存在 有

不用极限值说明极限存在. 可推广到左右极限及其他极限过程

连续函数

定义 在 某邻域内有定义, , 称函数 在 连续.

收敛于 ,

定理 反函数连续性定理: 设 在闭区间 上连续且严格单调增加, 记 , 则它的反函数 在 连续且严格单调增加

一致连续

定义 定义在区间 上的函数 , 有

选取与 无关, 区间内存在统一的度量

下凸函数在任意闭区间上 Lipschitz 连续.

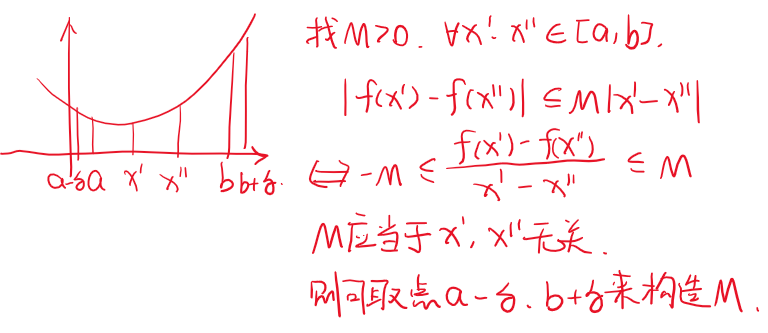
证明函数在区间上不一致连续, 利用否定

取一个 , 构造与 有关的 , 代入 并展开, 使其能大于

定理 一致连续 中数列 , , 有

自变量无限接近时, 函数值也要能无限接近. 作用当然是用来证不一致连续

闭区间上连续函数的性质

• Weierstrass 有界性: 在 上有界
• Weierstrass 最值: 在 上能取到最大值和最小值
• Bolzano-Cauchy 零点: 若 , 则
• Brouwer 不动点: 若 , 则
• Bolzano-Cauchy 中间值: 能取到介于最小值和最大值之间的任何一个值
• Cantor: 在 一致连续

存在 在 一致连续

简要证明 由 Cauchy 收敛,

在 一致连续,

, 要么 , 要么

Cauchy 收敛的形式很像一致连续. 注意定理的逆命题不成立, 如

许可协议

本文采用 署名-相同方式共享 4.0 国际 许可协议，转载请注明出处。

分享文章