最优化算法速通 - 约束优化

等式约束

• 正则点: 对于满足等式约束的点 , 梯度向量 线性无关.
  • 是正则点
• 曲面 , 若 上所有点都是正则点, 则维数为
• 切线空间 , 即 的零空间.
  • 正则点的切空间维数是
  • 切平面
• 法线空间
  • 正则点的法线空间的维数是
  • 法平面
• 切线空间和法线空间互为正交补

Lagrange 条件

若 是极大点则满足 和 平行, 即

Lagrange 定理: 若 是正则点, 则 , 使得

是局部极小点的必要条件

Lagrange函数

若 是极值点, 则 , 满足 . Lagrange 定理的必要条件等价于将 Lagrange 函数视为无约束优化问题得到的一阶必要条件.

Lagrange 函数关于 的 Hessian 矩阵:

• 二阶必要条件:
• 二阶充分条件:

二次规划

等价于

二次规划标准型

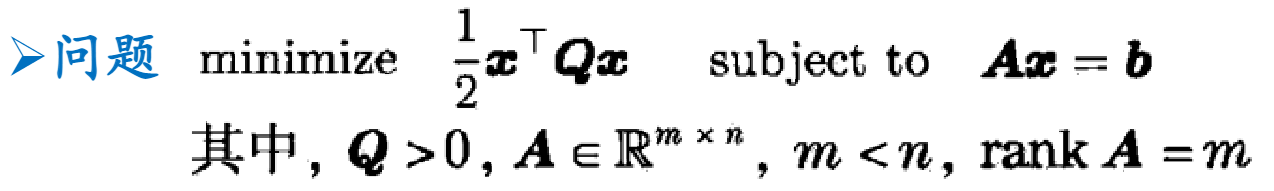
Lagrange 函数

Lagrange 条件

解得

一定满足二阶充分条件.

不等式约束

• 积极约束, 非积极约束: 不等式是否取等
• 正则点除了考虑等式约束线性无关, 不等式约束梯度也要线性无关.

KKT 条件

设 是正则点和局部极小点, 则 , 使得

1. 原始可行性:
2. 对偶可行性:
3. 原始最优性:
4. 互补松弛条件:

二阶条件

起作用约束构成曲面的切空间

• 二阶必要条件:
• 二阶充分条件:

对偶问题

原问题 Lagrange 函数:

鞍点 是 Lagrange 函数关于 的极小值点, 关于 的极大值点

原问题:

对偶问题:

注意到对偶问题的内层 是关于 的无约束优化问题, 目标函数是凹函数

弱对偶定理: 是原问题可行解, 是对偶问题可行解, 则

即

对偶问题的解是原问题的解的下界.

强对偶定理: 上式取等 Lagrange 函数存在鞍点

求解方法

投影方法

希望使无约束优化的迭代格式 能够满足约束条件

投影: 设 是非空闭凸集, 任意 在 上的投影为

• 是非空闭凸集, 投影存在且唯一
• • 当且仅当 是仿射流行时取等
• 是非扩张映射,
• 投影映射本身可能很难求

投影下的迭代格式:

投影梯度法:

• 仿射约束集 上的投影梯度法产生的迭代点满足
• 线性规划使用投影梯度法, 只要步长足够大, 一步就能得到最优解

Lagrange 法

Lagrange 函数:

使用梯度法, 每步关于 极小化, 关于 极大化:

对于不等式约束的情况

Lagrange 函数:

使用梯度法关于 极小化, 投影梯度法关于 极大化

罚函数法

指示函数

是罚函数, 需满足

1. 连续

罚参数 越大, 则逼近程度越好.

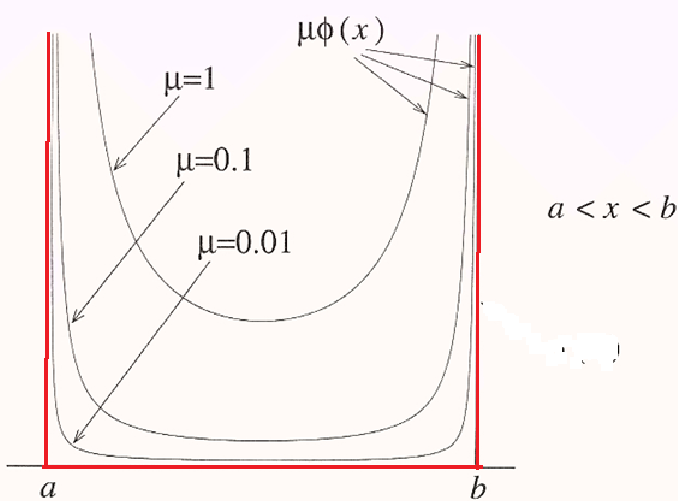
增广 Lagrange 函数

把 Lagrange 函数与罚函数结合，解决罚参数过大问题

许可协议

本文采用 署名-相同方式共享 4.0 国际 许可协议，转载请注明出处。

分享文章