最优化算法速通 - 线性规划

标准型

• 约束集：是凸多面体, 多胞形
• 凹函数在凸集上的极值点一定是集合的边界点, 线性规划的极值点一定是多胞形的顶点
• 解的存在性
  • 可行域为空集, 无最优解
  • 可行域为有界闭集, 最优解不唯一
  • 可行域为无界集, 不确定有无最优解

线性规划标准型:

其中

化为标准型:

1. 最大化转化为最小化相反数
2. 不等式约束引入松弛变量化为等式约束 (确保不等式只需大于等于0, 同时反转不等号方向)
3. 决策变量属于实数 时, 对分量进行非负拆分
4. 则两侧同乘 -1

线性规划的解

其中

从 中任选 个线性无关的列向量记作 , 则 , 则

• 在 下的基本解: 是 的一个解
• 基变量: 中的元素
• 基本列向量: 中的列向量
• 退化的基本解: 中有变量是 0
• 可行解: 满足约束条件
• 基本可行解:
  • 可以通过暴力枚举 (要保证 可逆)的方法求所有基本可行解
  • 最多有 个基本解
• 退化的基本可行解
• 最优可行解: 满足约束条件且使得 取得极小值

线性规划基本定理:

1. 存在可行解 存在基本可行解
2. 存在最优可行解 存在最优基本可行解

则可以通过搜索有限数量的基本可行解来求解线性规划问题. 但直接枚举复杂度很高, 需要更好的做法

解的性质:

• 基本可行解 非零分量对应的列向量组线性无关 在可行域的顶点处取得
• 最优解一定在可行域的顶点处取得

单纯形法

从某个基本可行解变换到另一个基本可行解, 直到找到最优基本可行解.

转轴元素

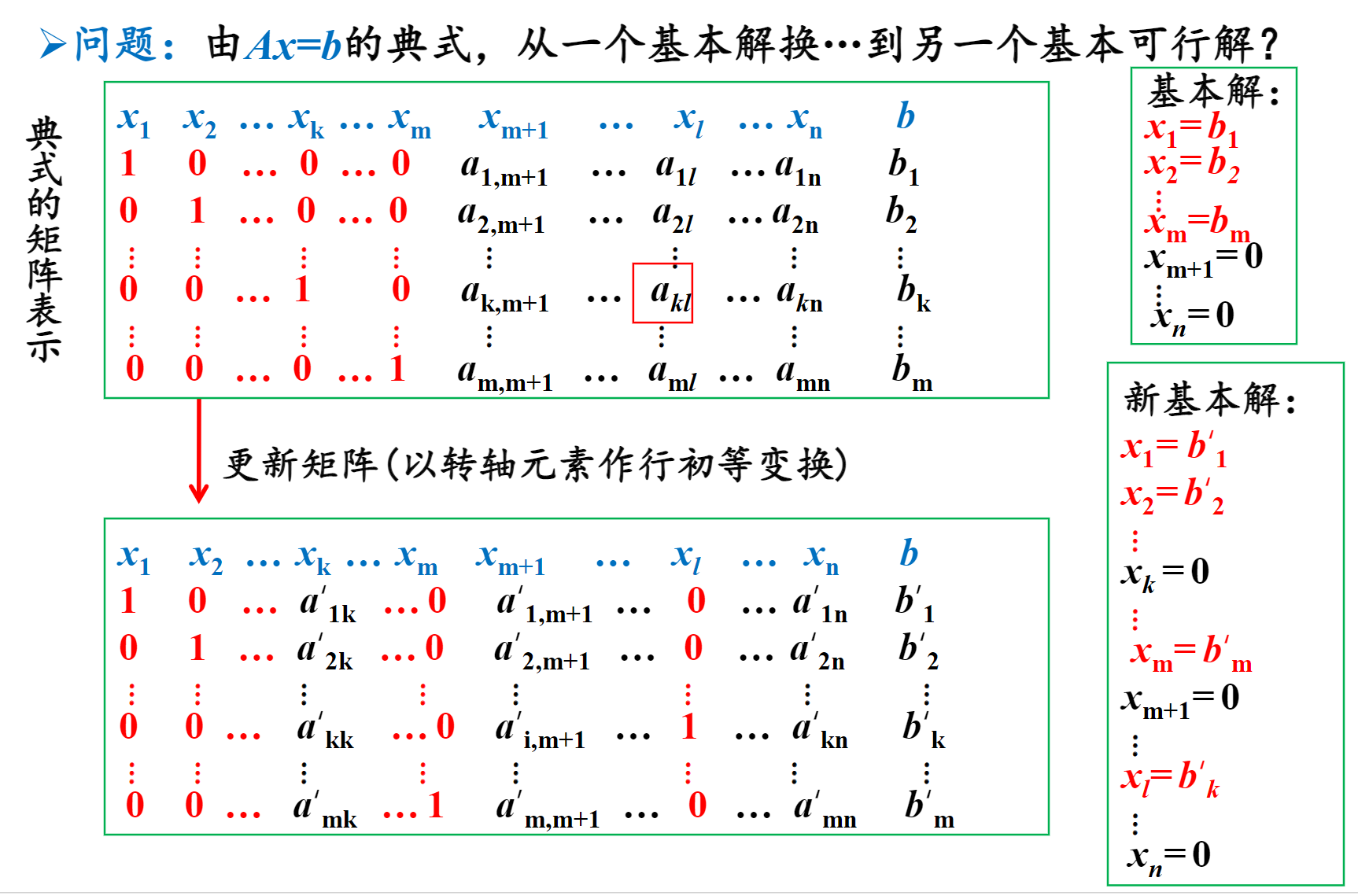
行的选择: 希望能保证变换后 , 保证基本解的可行性. 于是在第 列中选择满足以下条件的元素:

这样能使得 尽量大:

判断解的最优性

设 的前 列 是基向量, , , , 约束条件:

1. 若 , 则为基本可行解, , 目标函数值:
2. 若 , 则 . 定义 , 则目标函数值

则 最优解. 若 中存在负分量, 则将 中相应的值从 0 变为正数, 目标函数值就能变小, 通过转轴运算更新一次矩阵

单纯形表的矩阵表示

线性规划的基、基变量、基本可行解、判别式、函数值都在最后一个矩阵中.

将初始单纯形表转化为标准单纯形表, 需要做行初等变换使得基变量所在列的判别式值为 0, 然后进行单纯形表的操作：

1. 若上述矩阵中的判别式全部非负，则此时的基本解就是最优解，最优值的相反数在矩阵的右下角
2. 若上述矩阵中的判别式有负元素，则取最小的负元素所在的列进基，做1次转轴运算, 同时通过行初等变换更新判别式的值

例子:

确定初始可行基

有些明显的初始可行基可以直接看出来, 有的不行, 穷举 个列向量不现实, 需要更好的方法.

两阶段法

P0 有基本可行解 P1 有最优解且最有函数值为 0

1. (第一阶段) P1 初始时基变量全部位于人工变量中, 基变量的判别式均为 1
2. 通过行初等变换化为标准单纯形表, 使得基变量的判别式为 0
3. 做转轴变换直到求出最优解
   1. 若最优解不为 0 则无解
   2. 若有基变量在人工变量中
      1. 若这一行 , 则直接删除行
      2. 否则任选一个非零 做转轴变换使得人工变量出基
4. 删除人工变量的列
5. (第二阶段) 根据最小判别数不断做转轴运算求最优解.

若 , 则 P0 无解.

大 M 方法

加入至多 个人工变量 使得能找出一组基, 求解含参 线性规划问题, 使用判别数时认为 时无穷大, 得到的解就是原问题的解.

对偶线性规划

原问题 (P):

对偶问题 (D):

• 弱对偶定理: 原问题可行解, 对偶问题可行解,
• 若 , 则 和 是各自问题的最优解
• 如果 (P) 问题有最优解，那么 (D) 问题也有最优解，并且它们的最优函数值相同

互补松弛定理: 可行解 和 是最优解

许可协议

本文采用 署名-相同方式共享 4.0 国际 许可协议，转载请注明出处。

分享文章