最优化算法速通 - 凸集和凸函数

几何概念

• 线段:
• 超平面:
  • , 是法向量, 是截距
  • , 是平面上一点
• 半空间
  • 正半空间
  • 负半空间
• 线性簇: 线性方程组的解集

凸集

• 定义: 任意两点间的线段 (凸组合) 位于集合内
• 空集, 单点集, 线性簇是凸集
• 半正定矩阵集是凸集
• 保凸运算
  • 数乘, Minkowoski 和(任意两个不同集的向量相加得到新集合), 交集
  • 仿射变换
• 极点: 不能表达成集合内两个点连线段的"内点"
• 邻域, 内点, 开集, 边界, 闭集, 紧集
• 极值原理: 连续函数在紧集上一定能取到闭集

多面体

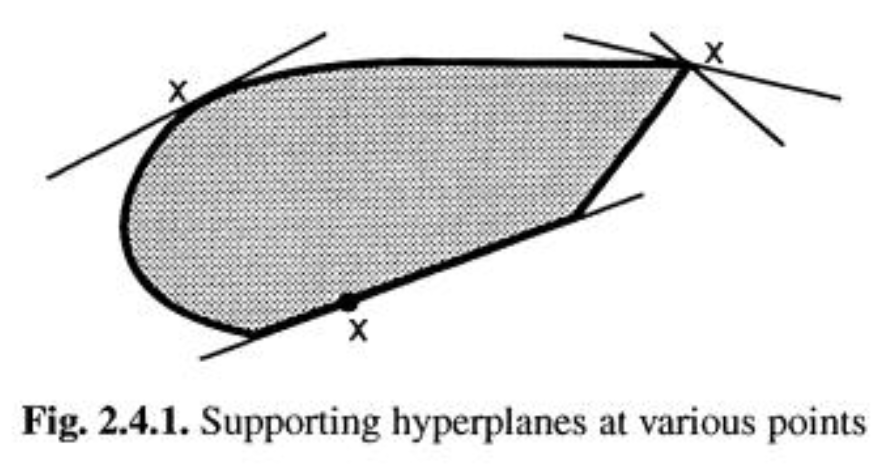
• 支撑超平面: 经过凸集的边界点, 使凸集完全位于一个半空间内
• 多面体: 可表示为有限个半空间的交集
• 非空有界的多面体:

序列与极限

• 矩阵序列 收敛于 :
• 矩阵收敛于零矩阵 矩阵的谱半径小于 1
• 矩阵的幂级数收敛 矩阵收敛于零矩阵
• 矩阵值函数 在某点连续且函数值可逆, 则存在邻域使得 存在且连续

可微性

仿射函数: 存在线性函数 和向量 , 使得

可微性: 理解为对函数仿射逼近 (一阶 Taylor 逼近)

• 一元函数时, 退化为一元函数的导数
• 多元函数时, 退化为多元函数的梯度

• 列向量
• 行向量

向量值函数 的导数 (Jacobi 矩阵 ):

纵轴(第一维)是因变量, 横轴(第二维)是自变量

Hessian 矩阵: 梯度的 Jacobi 矩阵, 二阶导

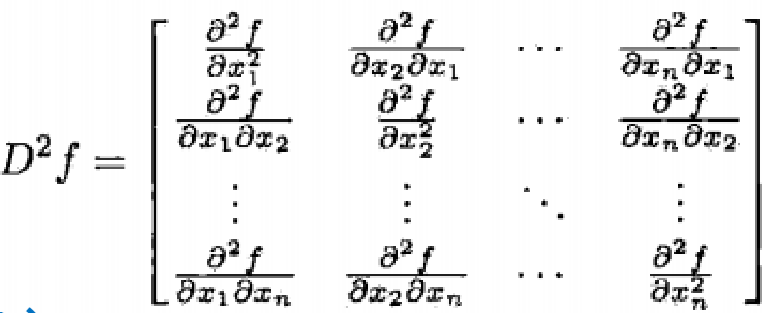
链式法则:

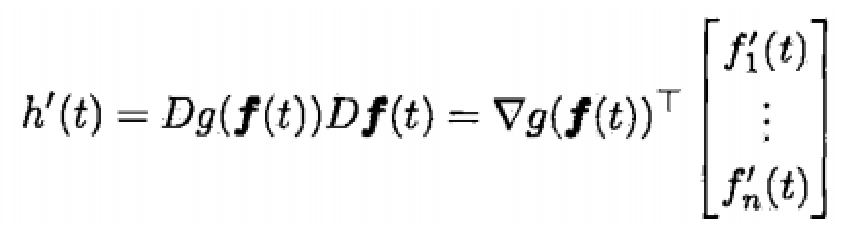
注意把向量的形状凑对, 求复合函数的 Jacobi, 只需外层 Jacobi 乘内层 Jacobi

方向导数: 单位方向向量点乘梯度

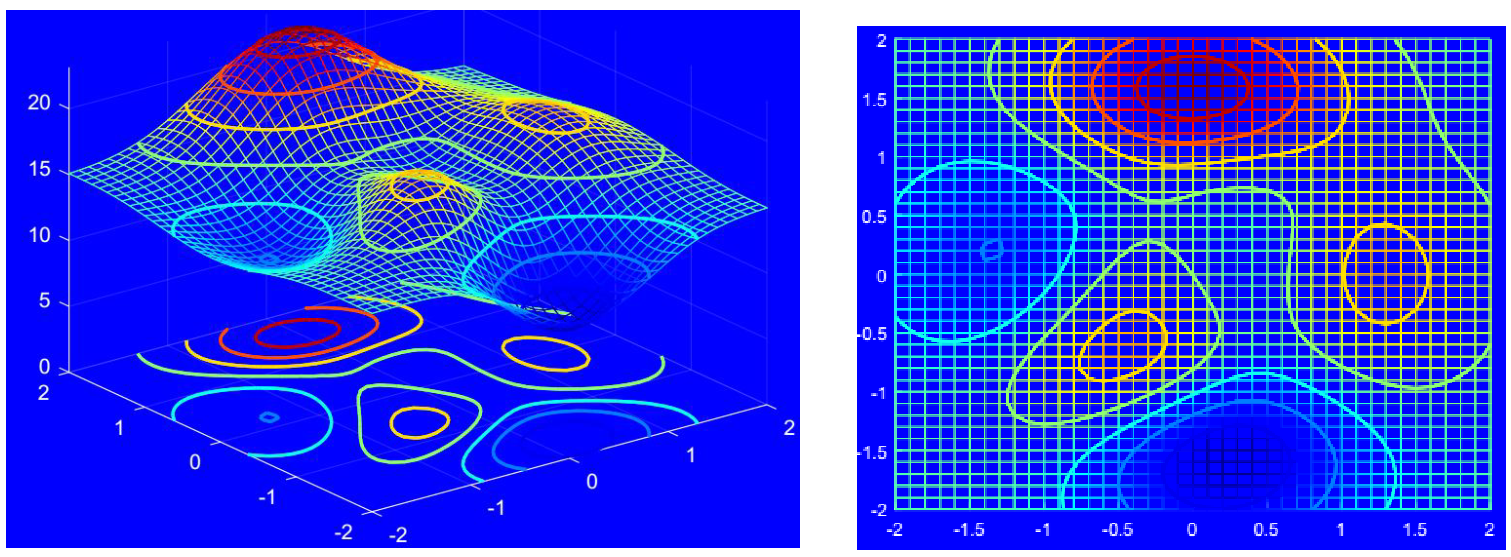
水平集

• 单值函数在水平 上的水平集(等值线):
  • 等值线不相交
  • 等值线疏密程度刻画函数变化快慢
  • 等值线与梯度垂直
  • 等值线在极值点附近近似为椭圆

Taylor 展开

可微函数 在 的切线超平面:

• 同阶无穷小 : 在原点的某邻域内有界
• 高阶无穷小 :

多元数量值函数的二阶 Taylor 展开 (假设二阶可微)

余项也可以是 . 更高阶的 Taylor 展开很难写出, 因为导数是高维张量.

中值定理 (类似 Lagrange 中值)

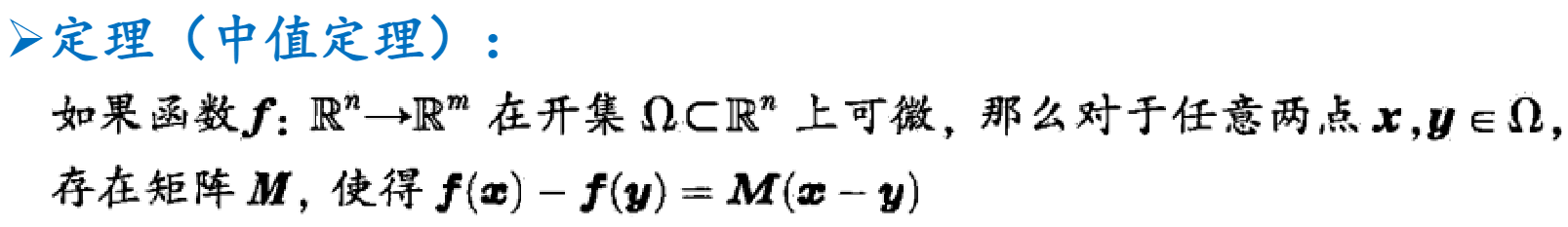
极小点

• 局部极小点: 去心邻域内
• 全局极小点:
• 严格局部极小点: 去心邻域内
• 严格全集极小点
• 可行方向 :

最优性条件

是局部极小点, 是任意可行方向

• 一阶必要条件:
  • 若 是内点, 则
• 二阶必要条件: 且
  • 若 是内点, 则 且 Hessian 矩阵半正定
• 二阶充分条件: 是内点, 则 且 Hessian 矩阵正定

许可协议

本文采用 署名-相同方式共享 4.0 国际 许可协议，转载请注明出处。

分享文章