复变函数速通 - 解析函数
复数
定义复数
共轭
模长
三角不等式
辐角
任何一个非零复数都有无穷个辐角
辐角主值: 在复数的辐角中把满足
三角表示法
指数表示法
求用复数方程表示的曲线: 代入
, 再通过平方, 取模等方法消除 , 得到关于 的方程. 最好先从几何意义上解释曲线.
定理 两复数相乘, 模长相乘, 辐角相加.
定理 两复数相除, 模数相除, 辐角相减.
有
但不一定有 ,
De Moivre 公式: 模长为
复平面上的点集
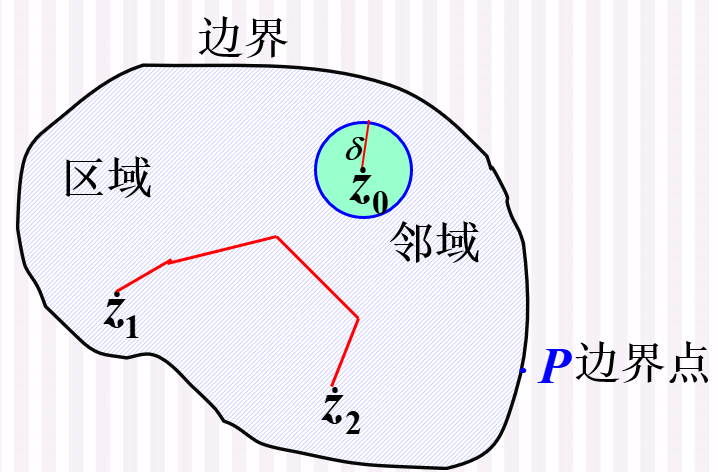
- 邻域:
- 无穷远点的邻域:
- 无穷远点的邻域:
- 去心邻域:
- 无穷远点的去心邻域:
- 无穷远点的去心邻域:
- 内点:
- 开集:
- 区域: 联通的开集
- 边界点: 不属于区域
- 边界:
- 边界可能是由几条曲线和孤立的点组成
- 闭区域: 区域连同边界
- 有界区域 / 无界区域: 是否可包含在以原点为中心的圆内
- 连续曲线:
- 光滑曲线:
- 简单曲线 / Jordan 曲线: 没有重点的连续曲线
- 简单曲线自身不相交
- 任意一条简单闭曲线将复平面唯一分成三个互不相交的点集
- 内部: 有界区域
- 外部: 无界区域
- 边界: 内部和外部的公共边界
- 单连通域: 在区域内任作一条简单闭曲线, 曲线内部总属于区域 (没有洞)
- 多连通域: 不是单连通域的区域
- 简单闭曲线的方向: 正向对应内部在左侧 (外边界逆时针, 内边界顺时针)
连续和极限
复变函数不区分函数, 映射, 变换等概念, 一个自变量对应的因变量可能不是唯一的.
定理
的方式是任意的.
许多实数列极限相关的定理对复数列极限仍成立, 如 Bolzano-Weierstrass 聚点定理, 闭集套定理, Heine-Borel 有限覆盖定理等.
定理
许多闭区间上连续函数的性质可推广到有界闭集上的连续复变函数, 如 Weierstrass 有界性和最值定理 (模长意义下), Cantor 一致连续性等等.
包括无穷远点在内的复平面称为扩充复平面. 可讨论广义极限和广义连续.
解析函数
定义 复变函数的导数:
的方式是任意的.
定义 在区域内处处可导, 则称
同实变函数, 可导一定连续, 连续不一定可导. 对于以复数
定理
定义
定义
定义 奇点: 在
函数在区域内解析
函数在区域内可导 函数在一点解析
函数在一点可导
- 解析函数的和差积商 (除去分母为零的点) 解析
- 解析函数的复合函数解析
- 所有多项式在复平面处处解析
- 有理分式函数子在分母不为零的点解析, 分母为零的点是奇点
Cauchy-Riemann 方程
定理
此时有导数公式
以及其他根据 C-R 方程导出的代换形式. 另外可结合二元实变函数可微的必要条件和充分条件:
由复变函数可微和可导的等价性, 在区域
事实上, 由解析函数的无穷可微性,
可微 连续, 满足 C-R 方程
极坐标的 C-R 方程
说明
初等解析函数
指数函数
定义满足以下条件的
记作
加法定理
可得到
的周期性, 周期是 这是实变函数 不具有的性质
三角函数
定义
正弦, 余弦函数的奇偶性, 周期 (
双曲函数
是以
初等多值函数
定义 单叶函数:
希望把多值函数的函数值限制到单叶函数, 以便研究, 可以使用
- 限制辐角法
- 割破平面法
根式函数
定义
的根是以原点为中心, 为半径的圆内接正 边形的 个顶点
根式函数的多值性:
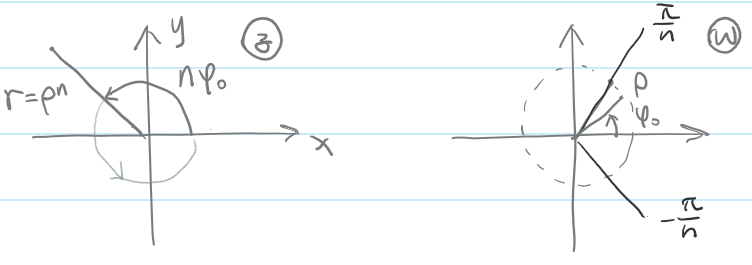
终边
将
限制辐角法
将
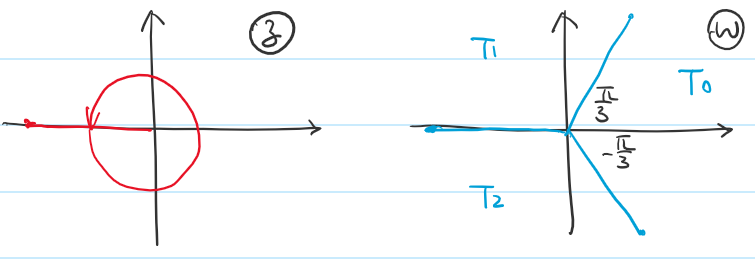
这样
然后可限制只取原函数落在某个特定单叶性区域的值, 即可将原函数转化为单叶函数. 式
割破平面法
根式函数出现多值性的原因是
考虑变点
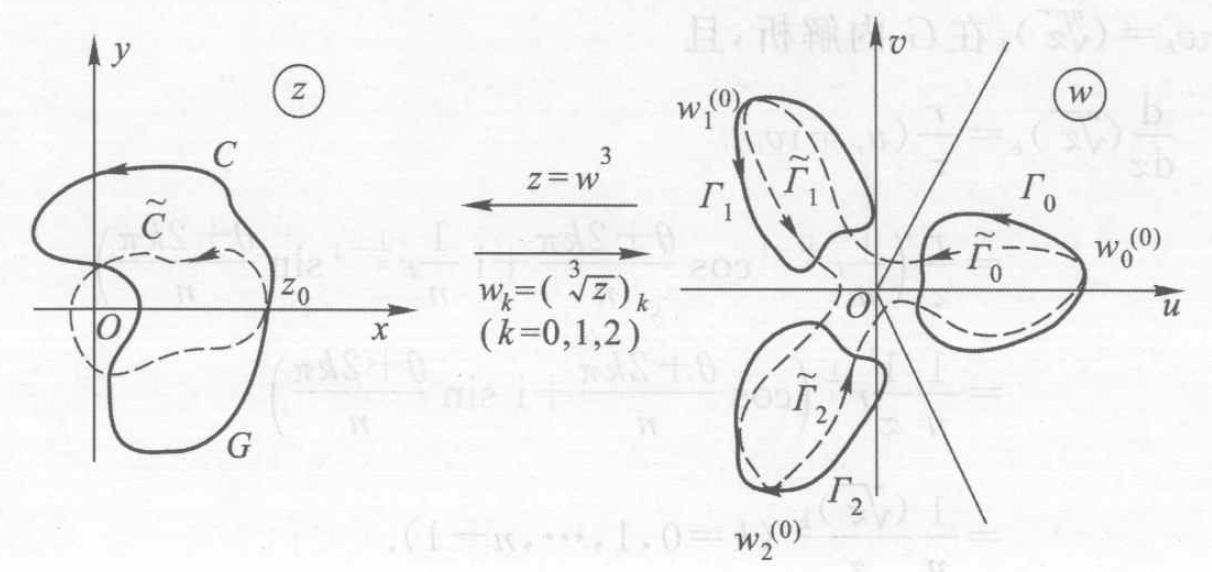
定义 多值函数的支点: 变点
有且仅有支点 若定义域不包括原点, 则不需要割破平面也能划分单值解析分支.
定义 支割线: 用来割破
对于支割线的不同做法, 得到的分支不同, 各分支的定义域随支割线变化. 每个单值分支在支割线上是不连续的, 在两岸取到不同的值, 可以扩充到单边连续到一岸.
定义 主值支:
对数函数
定义 对数函数是指数函数
负数无实对数, 正实数的复对数也是无穷多值的,
复对数仍然满足对数函数的基本性质 (集合相等)

导数是单值的
一般幂函数, 一般指数函数
定义 一般幂函数:
定义 一般指数函数:
具有有限个支点的函数
- 可能的支点是
说明
由单值解析分支上一点的初值


